Poor performance of bootstrap confidence intervals for the location of a quantitative trait locus

Abstract

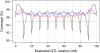
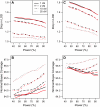
The aim of many genetic studies is to locate the genomic regions (called quantitative trait loci, QTL) that contribute to variation in a quantitative trait (such as body weight). Confidence intervals for the locations of QTL are particularly important for the design of further experiments to identify the gene or genes responsible for the effect. Likelihood support intervals are the most widely used method to obtain confidence intervals for QTL location, but the nonparametric bootstrap has also been recommended. Through extensive computer simulation, we show that bootstrap confidence intervals behave poorly and so should not be used in this context. The profile likelihood (or LOD curve) for QTL location has a tendency to peak at genetic markers, and so the distribution of the maximum-likelihood estimate (MLE) of QTL location has the unusual feature of point masses at genetic markers; this contributes to the poor behavior of the bootstrap. Likelihood support intervals and approximate Bayes credible intervals, on the other hand, are shown to behave appropriately.

Figure 1.—

Results for the chromosome 4 data of Sugiyama et al. (2001). (A) The LOD curve and the 1.5-LOD support interval. Tick marks at the bottom indicate the locations of the genetic markers. (B) A histogram of the estimated QTL locations in 10,000 bootstrap replicates, and the 95% bootstrap confidence interval, calculated by the method of Visscher et al. (1996).

Figure 2.—

Estimated distribution of the MLE of QTL location, , as a function of the true location of the QTL, θ, for θ varying from 45 to 50. The results are based on 10,000 simulation replicates of a backcross with 200 individuals for a chromosome of length 100 cM and having 11 equally spaced markers and with the heritability due to the QTL at 10%.

Figure 3.—

Coverage of 95% bootstrap confidence intervals (black), 1-LOD support intervals (red), and 95% Bayes credible intervals (blue) as a function of the true QTL position, θ. The dashed vertical gray lines denote marker positions on the chromosome.

Figure 4.—

Coverage of 95% bootstrap confidence intervals (black), 1-LOD support intervals (red), and 95% Bayes credible intervals (blue) as a function of the MLE of QTL position, . The dashed vertical gray lines denote marker positions on the chromosome.

Figure 5.—

Estimated amount to drop in a LOD support interval (A and C) and the nominal Bayes coverage for the approximate Bayes credible interval (B and D) to give 95% coverage, based on 100,000 simulation replicates. Backcross (A and B) and intercross (C and D) experiments with either 200 (black curves) or 500 (red curves) individuals were considered. The line types indicate different possible marker spacings. Values are plotted as a function of the effect of the QTL, scaled according to the power to detect the QTL.

Figure 6.—

Coverage of the 1.5-LOD support interval in a backcross (A), the 96.5% Bayes interval in a backcross (B), the 1.8-LOD support interval in an intercross (C), and the 97% Bayes interval in an intercross (D), based on 100,000 simulation replicates. The black curves are for 200 individuals; the red curves are for 500 individuals. The line types indicate different possible marker spacings. Values are plotted as a function of the effect of the QTL, scaled according to the power to detect the QTL.