Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2006 Apr;68(3):511-24.
doi: 10.1007/s11538-005-9034-4.

Mathematical models for hantavirus infection in rodents

Linda J S Allen  1 , Robert K McCormack, Colleen B Jonsson
Affiliations

Mathematical models for hantavirus infection in rodents

Linda J S Allen et al. Bull Math Biol. 2006 Apr.

Abstract

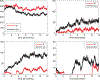
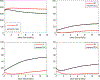
Hantavirus pulmonary syndrome is an emerging disease of humans that is carried by wild rodents. Humans are usually exposed to the virus through geographically isolated outbreaks. The driving forces behind these outbreaks is poorly understood. Certainly, one key driver of the emergence of these viruses is the virus population dynamics within the rodent population. Two new mathematical models for hantavirus infection in rodents are formulated and studied. The new models include the dynamics of susceptible, exposed, infective, and recovered male and female rodents. The first model is a system of ordinary differential equations while the second model is a system of stochastic differential equations. These new models capture some of the realistic dynamics of the male/female rodent hantavirus interaction: higher seroprevalence in males and variability in seroprevalence levels.

PubMed Disclaimer

Figures

Fig. 1
Fig. 1
Solution to the deterministic SEIR epidemic as a function of time. An endemic equilibrium for males: 357.1, 47.7, 76.2, 19.1, and females: 456.4, 14.5, 19.4. 9.7, is reached. The total population size at equilibrium equals the carrying capacity K = 1000. Seroprevalence is 12.5% at the endemic equilibrium.
Fig. 2
Fig. 2
One sample path of the stochastic SEIR epidemic model. The parameter values and initial conditions are the same as in Fig. 1.
Fig. 3
Fig. 3
An average of 1000 sample paths for the stochastic SEIR model. Compare this figure with Fig. 1. The average seroprevalence in year 2 is 10.4%.
See this image and copyright information in PMC

References

    1. Abramson G, Kenkre VM, 2002. Spatiotemporal patterns in hantavirus infection. Phys. Rev. E 66, 011912, 1–5. - PubMed
    1. Abramson G, Kenkre VM, Yates TL, Parmenter RR, 2003. Traveling waves of infection in the hantavirus epidemics. Bull. Math. Biol. 65, 519–534. - PubMed
    1. Allen EJ, 1999. Stochastic differential equations and persistence time for two interacting populations. Dyn. Cont. Discrete Impulsive Syst. 5, 271–281.
    1. Allen LJS, Allen EJ, 2003. A comparison of three different stochastic population models with regard to persistence time. Theor. Pop. Biol. 64, 439–449. - PubMed
    1. Allen LJS, 2003. An Introduction to Stochastic Processes with Applications to Biology. Prentice Hall: Upper Saddle River, N.J.

Publication types