Application of the method of fundamental solutions to potential-based inverse electrocardiography

Abstract

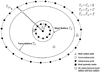
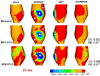
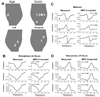
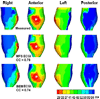
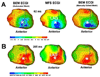
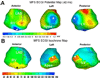
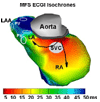
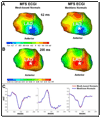
Potential-based inverse electrocardiography is a method for the noninvasive computation of epicardial potentials from measured body surface electrocardiographic data. From the computed epicardial potentials, epicardial electrograms and isochrones (activation sequences), as well as repolarization patterns can be constructed. We term this noninvasive procedure Electrocardiographic Imaging (ECGI). The method of choice for computing epicardial potentials has been the Boundary Element Method (BEM) which requires meshing the heart and torso surfaces and optimizing the mesh, a very time-consuming operation that requires manual editing. Moreover, it can introduce mesh-related artifacts in the reconstructed epicardial images. Here we introduce the application of a meshless method, the Method of Fundamental Solutions (MFS) to ECGI. This new approach that does not require meshing is evaluated on data from animal experiments and human studies, and compared to BEM. Results demonstrate similar accuracy, with the following advantages: 1. Elimination of meshing and manual mesh optimization processes, thereby enhancing automation and speeding the ECGI procedure. 2. Elimination of mesh-induced artifacts. 3. Elimination of complex singular integrals that must be carefully computed in BEM. 4. Simpler implementation. These properties of MFS enhance the practical application of ECGI as a clinical diagnostic tool.

FIGURE 1.

A schematic showing the configuration of fictitious points for a multi-connected domain. The dashed lines are the auxiliary surfaces that contain the fictitious points (virtual sources) marked by black circles. The filled square is the geometrical center of the “heart”, the empty triangle is located on the “heart surface” and the empty square on the “torso surface,” the two black circles on their connecting line at the auxiliary surfaces are the corresponding virtual source points.

FIGURE 2.

Canine epicardial potential maps 25 ms after pacing from a single anterior site (indicated by the asterisk *). Top row shows the directly measured epicardial potentials (four views) displaying the negative region (dark blue) around the pacing site, and two flanking positive maxima (red). Middle rows shows the noninvasively reconstructed potentials computed using MFS ECGI; note close similarity of noninvasive and invasive data. Bottom row shows the reconstruction using BEM ECGI.

FIGURE 3.

Canine epicardial electrograms (measured and computed using MFS ECGI) from selected locations on the heart surface for pacing from the same single site as in Fig. 2 (indicated by the asterisk). (A) Four views of epicardial surface. Numbers identify locations of the electrograms in the other panels. Measured (left column) and computed (right column) electrograms are compared in B, C and D. Number on the bottom left of each panel identifies the electrogram location (corresponding to numbers in A). (B) Monophasic (Q wave) electrograms from sites 1, 2 and 3. (C) Biphasic electrograms from sites 4, 5 and 6. (D) Monophasic (R wave) electrograms from sites 7, 8 and 9. CC is the Correlation Coefficient between invasive and noninvasive electrograms, indicating high level of similarity.

FIGURE 4.

Canine epicardial isochrone map for pacing from the same single site as in Fig. 2 (indicated by the asterisk). Top row shows the directly measured isochrones (four views) displaying the anterior pacing site. Middle row shows the noninvasively reconstructed isochrone map computed using MFS ECGI. Bottom row shows the noninvasively reconstructed isochrone map computed using BEM ECGI.

FIGURE 5.

Panel A: Human epicardial potential map (anterior view) 62 ms after pacing from a single RV endocardial site (marked by the asterisk). Left: BEM ECGI reconstruction with initial mesh (non-optimized), showing fragmentation of the negative region (blue) caused by meshing artifact. Middle: MFS ECGI reconstructs a single continuous minimum (blue) associated with single-site pacing. Right: BEM ECGI reconstruction with manually-edited mesh, showing that fragmentation is mesh related. Panel B: Human epicardial potential map (anterior view) during repolarization for pacing from the same site (205 ms after pacing).

FIGURE 6.

Human epicardial potential map and isochrone map for simultaneous RV and LV pacing (pacing sites marked by the asterisks *; note that the left and posterior views show the same pacing site). Panel A shows the MFS ECGI reconstructed potential map 40 ms after pacing (three partially overlapping views). Typical quasi-elliptic negative region (blue) surrounds each pacing site. Panel B shows the corresponding MFS ECGI reconstructed isochrone map in the same format.

FIGURE 7.

Normal human atrial activation isochrones reconstructed with MFS ECGI. RA: Right Atrium; LA: Left Atrium; LAA: Left Atrial Appendage; PV: Pulmonary Vein; SVC: Superior Vena Cava. Black arrows indicate direction of activation spread.

FIGURE 8.

Comparison of MFS ECGI reconstructions with mesh-based and meshless normal vectors. Panel A: Human epicardial potential map (anterior view) 62 ms after pacing from a single RV endocardial site (marked by the asterisk). Left: MFS ECGI reconstruction with normal vectors computed using a mesh. Right: MFS ECGI reconstruction with normal vectors computed without a mesh, using Radial Basis Function (RBF). Panel B: Human epicardial potential map (anterior view) during repolarization for pacing from the same site (205 ms after pacing). Same format as Panel A. Panel C: Human epicardial electrograms from selected locations on the heart surface for the same pacing dataset. Red traces show the MFS ECGI reconstruction with mesh-based normal vectors. Blue traces show the MFS ECGI reconstruction with meshless normal vectors computed using RBF.

FIGURE 9.

Panel A: Radial Basis Function (RBF) representation of the atrial surface in Fig. 7 and corresponding inflated/deflated surfaces. The RBF function grid values are shown on three orthogonal planes: x=60 (mm), y=90 (mm), and z=30 (mm). The original boundary is represented by the isosurface with RBF=0(mm). Since the positive normal direction is chosen inward, deflated surfaces are represented by isosurfaces with RBF>0 and inflated surfaces by the isosurfaces with RBF<0. Panel B: A deflated atrial surface obtained by selecting RBF=5 (mm). Blue circles represent the original boundary points, and red circles represent the deflated surface points; all red circles are enclosed by the 3D surface defined by the blue circles.