Packing, tiling, and covering with tetrahedra

Abstract

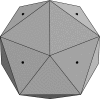
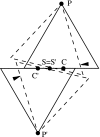
It is well known that three-dimensional Euclidean space cannot be tiled by regular tetrahedra. But how well can we do? In this work, we give several constructions that may answer the various senses of this question. In so doing, we provide some solutions to packing, tiling, and covering problems of tetrahedra. Our results suggest that the regular tetrahedron may not be able to pack as densely as the sphere, which would contradict a conjecture of Ulam. The regular tetrahedron might even be the convex body having the smallest possible packing density.

Fig. 1.

Certain arrangements of tetrahedra. (a) Five regular tetrahedra about a shared edge. The angle of the gap is 7.36°. (b) Twenty regular tetrahedra about a shared vertex. The gaps amount to 1.54 steradians.

Fig. 2.

Description of our notation. (a) Two adjacent cells of a cubic lattice and colorings of the two cubic sublattices of the BCC lattice as described in the text. (b) The Voronoi cell of a BCC lattice and the notation described in the text. The center of the cube is the origin of the coordinate system.

Fig. 3.

A portion of the densest (Bravais) lattice packing of regular tetrahedra (16). It has density Δ = 18/49 = 36.73 … %, and each tetrahedron is in contact with 14 others.

Fig. 4.

A portion of the densest uniform packing of regular tetrahedra that we have been able to find. It has density Δ = 2/3 = 66.666 … %.

Fig. 5.

A regular icosahedron inscribed in a truncated octahedron.

Fig. 6.

Each Scottish icosahedron is placed so that its eight contact spots coincide with those of its neighbors. It has density Δ = 82.13 … %.

Fig. 7.

For Betke and Henk’s displaced Scottish packing of icosahedra, the number of contact spots increases to 12. It has density Δ = 83.63574 … % and leads to the displaced Scottish regulars that have density Δ = 71.65598 … %.

Fig. 8.

Adjusting the Scottish regulars (a two-dimensional schematic).