ROC curves predicted by a model of visual search

Abstract

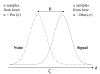
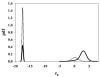
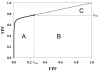
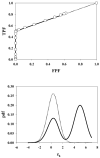
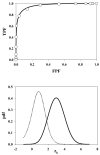
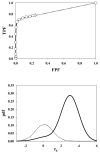
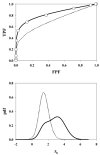
In imaging tasks where the observer is uncertain whether lesions are present, and where they could be present, the image is searched for lesions. In the free-response paradigm, which closely reflects this task, the observer provides data in the form of a variable number of mark-rating pairs per image. In a companion paper a statistical model of visual search has been proposed that has parameters characterizing the perceived lesion signal-to-noise ratio, the ability of the observer to avoid marking non-lesion locations, and the ability of the observer to find lesions. The aim of this work is to relate the search model parameters to receiver operating characteristic (ROC) curves that would result if the observer reported the rating of the most suspicious finding on an image as the overall rating. Also presented are the probability density functions (pdfs) of the underlying latent decision variables corresponding to the highest rating for normal and abnormal images. The search-model-predicted ROC curves are 'proper' in the sense of never crossing the chance diagonal and the slope is monotonically changing. They also have the interesting property of not allowing the observer to move the operating point continuously from the origin to (1, 1). For certain choices of parameters the operating points are predicted to be clustered near the initial steep region of the curve, as has been observed by other investigators. The pdfs are non-Gaussians, markedly so for the abnormal images and for certain choices of parameter values, and provide an explanation for the well-known observation that experimental ROC data generally imply a wider pdf for abnormal images than for normal images. Some features of search-model-predicted ROC curves and pdfs resemble those predicted by the contaminated binormal model, but there are significant differences. The search model appears to provide physical explanations for several aspects of experimental ROC curves.

Fig. 1

The search model for a single rating free-response study. The basic parameters of the model are μ, λ and ν, and s is the number of lesions per abnormal image. The two unit variance Gaussian distributions labeled Noise and Signal represent the pdfs of the z-samples from noise sites and signal sites, respectively. The number of noise sites n and the number of signal sites u are modeled by a Poisson and a Binomial distribution, respectively. The total number of decision sites per image in n+u. Each decision site yields a z-sample from the Noise or Signal distribution, for a noise site or a signal site, respectively. When a z-sample exceeds ζ, the observer's threshold, the observer marks the corresponding location. Noise site z-samples exceeding ζ are recorded as non-lesion localizations and corresponding signal site z-samples are recorded as lesion localizations.

Fig. 2

The pdfs of the decision variable z_h of the highest rated site for μ = 3, λ = 0.3, ν = 0.7 and s = 1. The dotted lines correspond to the normal cases and the solid lines to the abnormal cases. The delta functions at –infinity are for convenience shown as narrow Gaussians centered at −17.5. The two pdfs centered near 0 and 3 generate the continuously accessible portion of the ROC curve shown as the solid line in Fig. 3. The pdfs centered at -infinity generate the inaccessible portion of the ROC curve shown as the dotted line in Fig. 3.

Fig. 3

Geometrical interpretation of the area under the curve (AUC). The parameter values are as in Fig. 2. The area under the continuous section of the ROC curve, extending from (0, 0) to (x_max, y_max) and which is labeled A, corresponds to AUC₁ in Eqn. 12. The area of the rectangle labeled B is the contribution due to perfect discrimination between the abnormal image pdf in Fig. 2 and the delta function normal image pdf at -infinity. The area of the triangle labeled C is the contribution due to chance level discrimination between the two delta function pdfs at -infinity in Fig. 2. The sum of the areas B and C corresponds to AUC₂ in Eqn. 12.

Fig. 4

The ROC curve (upper panel) and pdfs (lower panel) for μ = 5, λ = 1, ν = 0.5 and s = 1. The open circles in the upper panel in this and succeeding plots are experimental ROC operating points from the simulations. The accessible portion of the ROC curve extends from (0, 0) to (0.63, 0.82). Note the strong bi-modality in the abnormal image pdf arising from the fact that half of the lesions are not hit. Therefore the highest decision variable for such images must have originated from a z-sample from N(0,1) yielding the peak near 0.

Fig. 5

The ROC curve and pdf for μ = 3, λ = 10, ν = 0.5 and s = 1. Due to the large value of λ the accessible section of the ROC curve extends almost to (1, 1). Also, the highest rating on abnormal images is likely due to a noise site z-sample, yielding the large peak in the abnormal image pdf near 1.5. A slight peak is also evident near z_h = 3 due to the fewer times when a signal site z-sample is the highest rating.

Fig. 6

The ROC curve predicted by the search model for μ = 3, λ = 3, ν = 1.0 and s = 1. This example most resembles a conventional ROC curve although strictly the accessible portion of the curve does not extend to (1, 1) and the pdfs are not exactly Gaussians.

Fig. 7

The ROC curve predicted by the search model for μ = 3, λ = 0.3, ν = 0.7 and s = 1. Due to the small value of λ, this example shows an unusually small accessible portion of the ROC curve which extends to (0.26, 0.78). The areas under the normal (abnormal) image pdfs are these values, namely 0.26 and 0.78, respectively. Note the clustering of the operating points near the initial vertical section of the ROC curve.

Fig. 8

The ROC curve predicted by the search model for μ = 3, λ = 10, ν = 0.5 and s = 2. Excepting for the number of lesions, the parameter values are identical to those shown in Fig. 5, which was for s = 1. The dotted curve corresponding to Fig. 5 is shown in the upper panel for convenience.