Size-dependent diffusion of membrane inclusions

Abstract

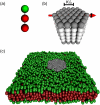
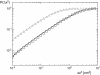
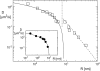
Experimentally determined diffusion constants are often used to elucidate the size and oligomeric state of membrane proteins and domains. This approach critically relies on the knowledge of the size-dependence of diffusion. We have used mesoscopic simulations to thoroughly quantify the size-dependent diffusion properties of membrane inclusions. For small radii R, we find that the lateral diffusion coefficient D is well described by the Saffman-Delbrück relation, which predicts a logarithmic decrease of D with R. However, beyond a critical radius Rc approximately hetam/(2etac) (h, bilayer thickness; etam/c, viscosity of the membrane/surrounding solvent) we observe significant deviations and the emergence of an asymptotic scaling D approximately 1/R2. The latter originates from the asymptotic hydrodynamics and the inclusion's internal degrees of freedom that become particularly relevant on short timescales. In contrast to the lateral diffusion, the size dependence of the rotational diffusion constant Dr follows the predicted hydrodynamic scaling Dr approximately 1/R2 over the entire range of sizes studied here.

FIGURE 1

(a) Model lipid as used in the simulations with implicit solvent (green, hydrophilic; red, hydrophobic). Hookean spring connections are indicated by cylindrical bonds. (b) Hexagonal membrane inclusion with edge length (K + 1)l₀ (K = 3). Dark/light gray corresponds to hydrophilic/hydrophobic beads; for clarity, Hookean connections are not shown. The red arrow highlights the orientation vector of the inclusion that was used to determine the rotational diffusion. (c) Snapshot of a membrane with an embedded inclusion (K = 7) after simulation of ∼80 μs real time.

FIGURE 2

Integrated distribution P(Δx²) of squared distances Δx² traveled within a period τ = 0.8 μs for inclusions with K = 2 and K = 19 (solid and shaded lines, respectively). Best fits according to Eq. 3 are shown as symbols.

FIGURE 3

Lateral diffusion coefficient D as a function of the inclusion radius R (symbols) is well described by the Saffman-Delbrück relation Eq. 1 (solid line) for small radii. Beyond a critical radius R_c ≈ hη_m/(2η_c) (dash-dotted line), deviations become visible and the data are best described by Eq. 4 (dashed line). (Inset) The diffusion coefficient as obtained from the explicit-solvent model (•) is well described by Eq. 1 (solid line) for small radii.

FIGURE 4

Rotational diffusion coefficient D_rot is well described by Eq. 2 (solid line) in the implicit-solvent case and in the explicit-solvent model (inset).