Multi-area visuotopic map complexes in macaque striate and extra-striate cortex
- PMID: 16831455
- PMCID: PMC2248457
- DOI: 10.1016/j.visres.2006.03.006
Multi-area visuotopic map complexes in macaque striate and extra-striate cortex
Abstract
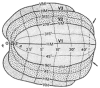
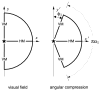
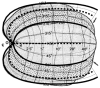
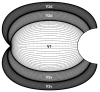
We propose that a simple, closed-form mathematical expression-the Wedge-Dipole mapping-provides a concise approximation to the full-field, two-dimensional topographic structure of macaque V1, V2, and V3. A single map function, which we term a map complex, acts as a simultaneous descriptor of all three areas. Quantitative estimation of the Wedge-Dipole parameters is provided via 2DG data of central-field V1 topography and a publicly available data set of full-field macaque V1 and V2 topography. Good quantitative agreement is obtained between the data and the model presented here. The increasing importance of fMRI-based brain imaging motivates the development of more sophisticated two-dimensional models of cortical visuotopy, in contrast to the one-dimensional approximations that have been in common use. One reason is that topography has traditionally supplied an important aspect of "ground truth," or validation, for brain imaging, suggesting that further development of high-resolution fMRI will be facilitated by this data analysis. In addition, several important insights into the nature of cortical topography follow from this work. The presence of anisotropy in cortical magnification factor is shown to follow mathematically from the shared boundary conditions at the V1-V2 and V2-V3 borders, and therefore may not causally follow from the existence of columnar systems in these areas, as is widely assumed. An application of the Wedge-Dipole model to localizing aspects of visual processing to specific cortical areas-extending previous work in correlating V1 cortical magnification factor to retinal anatomy or visual psychophysics data-is briefly discussed.
Figures




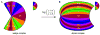
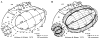










Similar articles
-
The V1 -V2-V3 complex: quasiconformal dipole maps in primate striate and extra-striate cortex.Neural Netw. 2002 Dec;15(10):1157-63. doi: 10.1016/s0893-6080(02)00094-1. Neural Netw. 2002. PMID: 12425434
-
Retinotopic mapping of the peripheral visual field to human visual cortex by functional magnetic resonance imaging.Hum Brain Mapp. 2012 Jul;33(7):1727-40. doi: 10.1002/hbm.21324. Epub 2012 Mar 22. Hum Brain Mapp. 2012. PMID: 22438122 Free PMC article.
-
Visual topography of V2 in the macaque.J Comp Neurol. 1981 Oct 1;201(4):519-39. doi: 10.1002/cne.902010405. J Comp Neurol. 1981. PMID: 7287933
-
Visual field representation in striate and prestriate cortices of a prosimian primate (Galago garnetti).J Neurophysiol. 1997 Jun;77(6):3193-217. doi: 10.1152/jn.1997.77.6.3193. J Neurophysiol. 1997. PMID: 9212268
-
Human cortical areas underlying the perception of optic flow: brain imaging studies.Int Rev Neurobiol. 2000;44:269-92. doi: 10.1016/s0074-7742(08)60746-1. Int Rev Neurobiol. 2000. PMID: 10605650 Review.
Cited by
-
Population response to natural images in the primary visual cortex encodes local stimulus attributes and perceptual processing.J Neurosci. 2012 Oct 3;32(40):13971-86. doi: 10.1523/JNEUROSCI.1596-12.2012. J Neurosci. 2012. PMID: 23035105 Free PMC article.
-
A new psychophysical estimation of the receptive field size.Neurosci Lett. 2008 Jun 20;438(2):246-51. doi: 10.1016/j.neulet.2008.04.040. Epub 2008 May 6. Neurosci Lett. 2008. PMID: 18467028 Free PMC article.
-
Estimation of cortical magnification from positional error in normally sighted and amblyopic subjects.J Vis. 2015 Feb 26;15(2):25. doi: 10.1167/15.2.25. J Vis. 2015. PMID: 25761341 Free PMC article.
-
Heterogeneous Effects of Cognitive Arousal on the Contrast Response in Human Visual Cortex.J Neurosci. 2025 Jun 18;45(25):e0798242025. doi: 10.1523/JNEUROSCI.0798-24.2025. J Neurosci. 2025. PMID: 40280712 Free PMC article.
-
Infants' visual system nonretinotopically integrates color signals along a motion trajectory.J Vis. 2015 Jan 26;15(1):15.1.25. doi: 10.1167/15.1.25. J Vis. 2015. PMID: 25624464
References
-
- Adams DL, Horton JC. “What you see …”, review of Visual Disturbances following Gunshot Wounds of the Cortical Visual Areaby Tatsuji Inouye (M. Glickstein, & M. Fahle, Trans) Nature. 2001;412(6846):482–483.
-
- Adams DL, Horton JC. Capricious expression of cortical columns in the primate brain. Nature Neuroscience. 2003a;6(2):113–114. - PubMed
-
- Ahlfors LV. Complex analysis. 2. New York: McGraw-Hill; 1966a.
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

