Dynamics, energetics, and structure in protein folding

Abstract

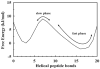
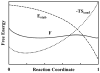
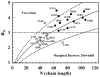
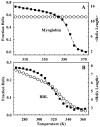
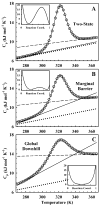
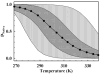
For many decades, protein folding experimentalists have worked with no information about the time scales of relevant protein folding motions and without methods for estimating the height of folding barriers. Protein folding experiments have been interpreted using chemical models in which the folding process is characterized as a series of equilibria between two or more distinct states that interconvert with activated kinetics. Accordingly, the information to be extracted from experiments was circumscribed to apparent equilibrium constants and relative folding rates. Recent developments are changing this situation dramatically. The combination of fast-folding experiments with the development of analytical methods more closely connected to physical theory reveals that folding barriers in native conditions range from minimally high (approximately 14RT for the very slow folder AcP) to nonexistent. While slow-folding (i.e., > or = 1 ms) single-domain proteins are expected to fold in a two-state fashion, microsecond-folding proteins should exhibit complex behavior arising from crossing marginal or negligible folding barriers. This realization opens a realm of exciting opportunities for experimentalists. The free energy surface of a protein with a marginal (or no) barrier can be mapped using equilibrium experiments, which could resolve energetic factors from structural factors in folding. Kinetic experiments on these proteins provide the unique opportunity to measure folding dynamics directly. Furthermore, the complex distributions of time-dependent folding behaviors expected for these proteins might be accessible to single-molecule measurements. Here, we discuss some of these recent developments in protein folding, emphasizing aspects that can serve as a guide for experimentalists interested in exploiting this new avenue of research.

Figure 1

One dimensional free energy surface for α-helix formation obtained by projecting the free energy of all of the species from the detailed kinetic model as a function of the number of helical peptide bonds. The arrows represent the main flux involved in each of the two observable kinetic phases.

Figure 2

Representation of a one-dimensional folding free energy surface: stabilization free energy (dashed line); conformational entropy contribution (dotted line); and global free energy (continuous line). The height of the free energy barrier is ~20 kJ/mol.

Figure 3

Plot of the n_σ parameter versus the number of aminoacids (N) for several proteins with T_m near 333 K. Proteins are named with their pdb code. The continuous line shows the average n_σ at 333 K obtained using a ΔH = 2.92 kJ/mol per residue and ΔC_p = 58 J/(mol.K) per residue(83). The two dotted lines show the average n_σ at 318 K and 348 K to provide the swath of T_m values for the proteins used in the plot. The dashed line at n_σ = 3 sets an approximate threshold between two-state-like and marginal barriers.

Figure 4

Analysis of far-uv CD spectra as a function of protein unfolding for the two state protein myoglobin (A) and the global downhill protein BBL (B): average helical content (black squares, left scale); average helix length (open circles, right scale). Experiments were performed at 20 mM phosphate buffer pH 7.0. Each CD spectrum was fitted to the expression: $$\langle \theta (\lambda )\rangle =x_H·\left({\theta }_{\lambda }^{\infty }·(1-l_H/k_{\lambda })\right)+(1-x_H)·{\theta }_{\lambda }^{\mathit{coil}}$$ where x_H is the fraction helix, l_H is the average helix length, θ^∞is the mean residue ellipticity of an infinite length helix as a function of wavelength (obtained from Chen et al.(71)), k is the wavelength dependent helix dependence of the CD spectrum (from ref (71) and then further fitted to the lowest temperature CD spectrum with the known x_H and l_H from the structure. The latter was required to fine tune structural details on each particular protein. θ^coil is the mean residue ellipticity as a function of wavelength of a random coil (taken as the CD spectrum of the protein in fully denaturing conditions).

Figure 5

Simulated DSC thermograms for proteins with different folding barriers: A) two-state-like (midpoint barrier ~18 kJ/mol); B) Marginal barrier (midpoint barrier ~2 kJ/mol); C) Global downhill (no barrier at midpoint). The continuous curves are two-state fits to the simulated data with continuous and dashed lines representing the phenomenological baselines for the “native” and “unfolded” states, respectively. The dotted line shows the theoretical native heat capacity. Insets shows the free energy barrier at the midpoint.

Figure 6

Folding kinetics at different barrier heights: A) normalized relaxation kinetics in the folding direction (dotted lines) and unfolding direction (continuous lines) to the same final condition (near the midpoint); B) normalized relaxation kinetics with added noise and best fits to single exponential decays.

Figure 7

Equilibrium global downhill unfolding at atomic resolution. The circled line represents the average atomic unfolding behavior, or global unfolding behavior (i.e. the behavior observed with a low-resolution technique). The dark gray swath corresponds to atomic unfolding behaviors within one standard deviation of the average. The light gray swaths represent the maximal spread of individual atomic unfolding behaviors, which should roughly correspond to the broadness of the global unfolding transition.