Multivariate curve resolution of time course microarray data

Abstract

Background: Modeling of gene expression data from time course experiments often involves the use of linear models such as those obtained from principal component analysis (PCA), independent component analysis (ICA), or other methods. Such methods do not generally yield factors with a clear biological interpretation. Moreover, implicit assumptions about the measurement errors often limit the application of these methods to log-transformed data, destroying linear structure in the untransformed expression data.

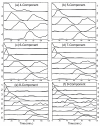
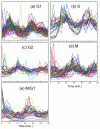
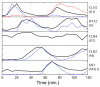
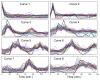
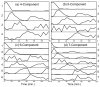
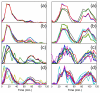
Results: In this work, a method for the linear decomposition of gene expression data by multivariate curve resolution (MCR) is introduced. The MCR method is based on an alternating least-squares (ALS) algorithm implemented with a weighted least squares approach. The new method, MCR-WALS, extracts a small number of basis functions from untransformed microarray data using only non-negativity constraints. Measurement error information can be incorporated into the modeling process and missing data can be imputed. The utility of the method is demonstrated through its application to yeast cell cycle data.

Conclusion: Profiles extracted by MCR-WALS exhibit a strong correlation with cell cycle-associated genes, but also suggest new insights into the regulation of those genes. The unique features of the MCR-WALS algorithm are its freedom from assumptions about the underlying linear model other than the non-negativity of gene expression, its ability to analyze non-log-transformed data, and its use of measurement error information to obtain a weighted model and accommodate missing measurements.

Figure 1

Simplified representation of the bilinear model. The expression levels of three genes as a function of time are represented as the linear combination of two underlying regualtory factors making up the profile matrix, P, and the contribution matrix, C, which determines how each gene responds to the individual regulatory factors.

Figure 2

MCR-WALS results (P matrix) for Alpha-696 data set. Profile vectors (normalized to unit length) extracted for models with 4 to 9 components are shown. The vectors are arranged in order of appearance of the first major peak in the profile.

Figure 3

Profiles of designated cell cycle regulated genes. Expression profiles (normalized to unit length) for the 292 cell cycle regulated genes identified by Spellman et al. [32] are shown grouped by the associated phase.

Figure 4

Comparison of MCR-WALS extracted profiles with designated cell cycle regulated genes. Selected profile vectors (dashed lines) extracted from the Alpha-696 data set with the 8-component model are compared with the time profiles for representative genes (solid lines) selected by Lu et al. [2] for each phase of the cell cycle. Both sets of profiles are normalized to unit length. Two extracted profiles were necessary to account for each cycle of the G1 phase and no clear match was indicated for G2.

Figure 5

Comparison of MCR-WALS extracted profiles with highly correlated gene expression profiles. Profile vectors extracted from the Alpha-696 data set with the 8-component model (thick dashed lines) are compared with the 40 most highly correlated gene expression profiles from the Alpha-full data set. All profiles are normalized to unit length.

Figure 6

MCR-ATLS results (P matrix) for Alpha-full data set. Profile vectors (normalized to unit length) extracted for models with 4 to 7 components are shown. The vectors are arranged in order of appearance of the first major peak in the profile.

Figure 7

Reproducibility of MCR-WALS results for two representative profiles from the six-component model. Profile vectors for two selected components of the six-component model extracted under different conditions. In each case, ten replicate runs were made. (a) Alpha 696, random initialization, (b) Alpha-696, random subsampling, (c) Alpha-full, random initialization, (d) Alpha-full, random subsampling.