Computational biology in the study of cardiac ion channels and cell electrophysiology
- PMID: 16848931
- PMCID: PMC1994938
- DOI: 10.1017/S0033583506004227
Computational biology in the study of cardiac ion channels and cell electrophysiology
Abstract
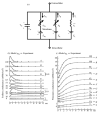
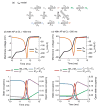
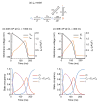
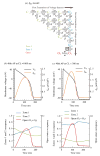
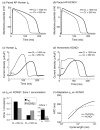
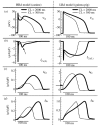
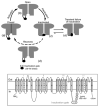
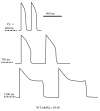
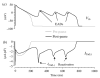
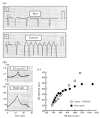
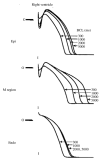
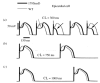
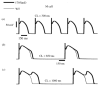
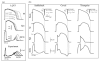
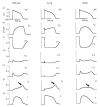
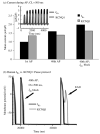
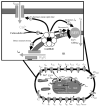
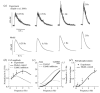
The cardiac cell is a complex biological system where various processes interact to generate electrical excitation (the action potential, AP) and contraction. During AP generation, membrane ion channels interact nonlinearly with dynamically changing ionic concentrations and varying transmembrane voltage, and are subject to regulatory processes. In recent years, a large body of knowledge has accumulated on the molecular structure of cardiac ion channels, their function, and their modification by genetic mutations that are associated with cardiac arrhythmias and sudden death. However, ion channels are typically studied in isolation (in expression systems or isolated membrane patches), away from the physiological environment of the cell where they interact to generate the AP. A major challenge remains the integration of ion-channel properties into the functioning, complex and highly interactive cell system, with the objective to relate molecular-level processes and their modification by disease to whole-cell function and clinical phenotype. In this article we describe how computational biology can be used to achieve such integration. We explain how mathematical (Markov) models of ion-channel kinetics are incorporated into integrated models of cardiac cells to compute the AP. We provide examples of mathematical (computer) simulations of physiological and pathological phenomena, including AP adaptation to changes in heart rate, genetic mutations in SCN5A and HERG genes that are associated with fatal cardiac arrhythmias, and effects of the CaMKII regulatory pathway and beta-adrenergic cascade on the cell electrophysiological function.
Figures

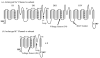



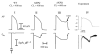




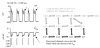


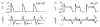

Similar articles
-
Rate dependence and regulation of action potential and calcium transient in a canine cardiac ventricular cell model.Circulation. 2004 Nov 16;110(20):3168-74. doi: 10.1161/01.CIR.0000147231.69595.D3. Epub 2004 Oct 25. Circulation. 2004. PMID: 15505083 Free PMC article.
-
HERG channel (dys)function revealed by dynamic action potential clamp technique.Biophys J. 2005 Jan;88(1):566-78. doi: 10.1529/biophysj.104.047290. Epub 2004 Oct 8. Biophys J. 2005. PMID: 15475579 Free PMC article.
-
Simulation of Ca-calmodulin-dependent protein kinase II on rabbit ventricular myocyte ion currents and action potentials.Biophys J. 2007 Dec 1;93(11):3835-47. doi: 10.1529/biophysj.107.114868. Epub 2007 Aug 17. Biophys J. 2007. PMID: 17704163 Free PMC article.
-
The molecular genetics of the long QT syndrome: genes causing fainting and sudden death.Annu Rev Med. 1998;49:263-74. doi: 10.1146/annurev.med.49.1.263. Annu Rev Med. 1998. PMID: 9509262 Review.
-
Sodium channel (dys)function and cardiac arrhythmias.Cardiovasc Ther. 2010 Oct;28(5):287-94. doi: 10.1111/j.1755-5922.2010.00210.x. Epub 2010 Jul 14. Cardiovasc Ther. 2010. PMID: 20645984 Review.
Cited by
-
Inversion and computational maturation of drug response using human stem cell derived cardiomyocytes in microphysiological systems.Sci Rep. 2018 Dec 4;8(1):17626. doi: 10.1038/s41598-018-35858-7. Sci Rep. 2018. PMID: 30514966 Free PMC article.
-
Human cardiac systems electrophysiology and arrhythmogenesis: iteration of experiment and computation.Europace. 2014 Nov;16 Suppl 4(Suppl 4):iv77-iv85. doi: 10.1093/europace/euu264. Europace. 2014. PMID: 25362174 Free PMC article. Review.
-
A computational method for identifying an optimal combination of existing drugs to repair the action potentials of SQT1 ventricular myocytes.PLoS Comput Biol. 2021 Aug 12;17(8):e1009233. doi: 10.1371/journal.pcbi.1009233. eCollection 2021 Aug. PLoS Comput Biol. 2021. PMID: 34383746 Free PMC article.
-
Hodgkin-Huxley revisited: reparametrization and identifiability analysis of the classic action potential model with approximate Bayesian methods.R Soc Open Sci. 2015 Dec 23;2(12):150499. doi: 10.1098/rsos.150499. eCollection 2015 Dec. R Soc Open Sci. 2015. PMID: 27019736 Free PMC article.
-
Computational modeling of cardiac electrophysiology and arrhythmogenesis: toward clinical translation.Physiol Rev. 2024 Jul 1;104(3):1265-1333. doi: 10.1152/physrev.00017.2023. Epub 2023 Dec 28. Physiol Rev. 2024. PMID: 38153307 Free PMC article. Review.
References
-
- Abbott GW, Sesti F, Splawski I, Buck ME, Lehmann MH, Timothy KW, Keating MT, Goldstein SA. MiRP1 forms IKr potassium channels with HERG and is associated with cardiac arrhythmia. Cell. 1999;97:175–187. - PubMed
-
- Abriel H, Cabo C, Wehrens XH, Rivolta I, Motoike HK, Memmi M, Napolitano C, Priori SG, Kass RS. Novel arrhythmogenic mechanism revealed by a long-QT syndrome mutation in the cardiac Na(+) channel. Circulation Research. 2001;88:740–745. - PubMed
-
- Antzelevitch C. The Brugada syndrome: ionic basis and arrhythmia mechanisms. Journal of Cardiovascular Electrophysiology. 2001;12:268–272. - PubMed
-
- Antzelevitch C, Dumaine R. Electrical heterogeneity in the heart: physiological, pharmacological and clinical implications. In: Page E, Fozzard H, Solaro J, editors. Handbook of Physiology, Section 2 The Cardiovascular System. The Heart. I. New York: Oxford University Press; 2002. pp. 654–692.
-
- Antzelevitch C, Fish J. Electrical heterogeneity within the ventricular wall. Basic Research in Cardiology. 2001;96:517–527. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Miscellaneous

