Space and contact networks: capturing the locality of disease transmission
- PMID: 16849245
- PMCID: PMC1664645
- DOI: 10.1098/rsif.2005.0105
Space and contact networks: capturing the locality of disease transmission
Abstract
While an arbitrary level of complexity may be included in simulations of spatial epidemics, computational intensity and analytical intractability mean that such models often lack transparency into the determinants of epidemiological dynamics. Although numerous approaches attempt to resolve this complexity-tractability trade-off, moment closure methods arguably offer the most promising and robust frameworks for capturing the role of the locality of contact processes on global disease dynamics. While a close analogy may be made between full stochastic spatial transmission models and dynamic network models, we consider here the special case where the dynamics of the network topology change on time-scales much longer than the epidemiological processes imposed on them; in such cases, the use of static network models are justified. We show that in such cases, static network models may provide excellent approximations to the underlying spatial contact process through an appropriate choice of the effective neighbourhood size. We also demonstrate the robustness of this mapping by examining the equivalence of deterministic approximations to the full spatial and network models derived under third-order moment closure assumptions. For systems where deviation from homogeneous mixing is limited, we show that pair equations developed for network models are at least as good an approximation to the underlying stochastic spatial model as more complex spatial moment equations, with both classes of approximation becoming less accurate only for highly localized kernels.
Figures

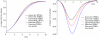
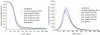
Similar articles
-
Analytic approximation of spatial epidemic models of foot and mouth disease.Theor Popul Biol. 2008 May;73(3):349-68. doi: 10.1016/j.tpb.2007.12.010. Epub 2008 Jan 19. Theor Popul Biol. 2008. PMID: 18313709
-
Deterministic epidemic models on contact networks: correlations and unbiological terms.Theor Popul Biol. 2011 Jun;79(4):115-29. doi: 10.1016/j.tpb.2011.01.004. Epub 2011 Feb 23. Theor Popul Biol. 2011. PMID: 21354193
-
Pair-level approximations to the spatio-temporal dynamics of epidemics on asymmetric contact networks.J Math Biol. 2006 Jul;53(1):61-85. doi: 10.1007/s00285-006-0377-3. Epub 2006 Apr 24. J Math Biol. 2006. PMID: 16791650
-
Large-scale spatial-transmission models of infectious disease.Science. 2007 Jun 1;316(5829):1298-301. doi: 10.1126/science.1134695. Science. 2007. PMID: 17540894 Review.
-
Modeling epidemics: A primer and Numerus Model Builder implementation.Epidemics. 2018 Dec;25:9-19. doi: 10.1016/j.epidem.2018.06.001. Epub 2018 Jul 13. Epidemics. 2018. PMID: 30017895 Review.
Cited by
-
Epigrass: a tool to study disease spread in complex networks.Source Code Biol Med. 2008 Feb 26;3:3. doi: 10.1186/1751-0473-3-3. Source Code Biol Med. 2008. PMID: 18302744 Free PMC article.
-
Connecting network properties of rapidly disseminating epizoonotics.PLoS One. 2012;7(6):e39778. doi: 10.1371/journal.pone.0039778. Epub 2012 Jun 25. PLoS One. 2012. PMID: 22761900 Free PMC article.
-
Infectious disease transmission as a forensic problem: who infected whom?J R Soc Interface. 2013 Feb 6;10(81):20120955. doi: 10.1098/rsif.2012.0955. Print 2013 Apr 6. J R Soc Interface. 2013. PMID: 23389896 Free PMC article.
-
Mathematical models of infectious disease transmission.Nat Rev Microbiol. 2008 Jun;6(6):477-87. doi: 10.1038/nrmicro1845. Nat Rev Microbiol. 2008. PMID: 18533288 Free PMC article. Review.
-
On spatially explicit models of cholera epidemics.J R Soc Interface. 2010 Feb 6;7(43):321-33. doi: 10.1098/rsif.2009.0204. Epub 2009 Jul 15. J R Soc Interface. 2010. PMID: 19605400 Free PMC article.
References
-
- Albert R, Barabási A.-L. Statistical mechanics of complex networks. Rev. Mod. Phys. 2002;74:47–97. doi:10.1103/RevModPhys.74.47 - DOI
-
- Anderson R.M, Gupta S. The significance of sexual partner contact networks for the transmission dynamics of HIV. J. Acquir. Immune Defic. Syndr. 1990;3:417–429. - PubMed
-
- Anderson R.M, May R.M. Oxford University Press; Oxford, UK: 1992. Infectious diseases of humans: dynamics and control.
-
- Barrat A, Barthelemy M, Pastor-Satorras R, Vespignani A. The architecture of complex weighted networks. Proc. Natl Acad. Sci. USA. 2004;101:3747–3752. doi:10.1073/pnas.0400087101 - DOI - PMC - PubMed
-
- Bauch C.T, Galvani A.P. Using network models to approximate spatial point-process models. Math. Biosci. 2003;184:101–114. doi:10.1016/S0025-5564(03)00042-7 - DOI - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Medical

