Optical trapping
- PMID: 16878180
- PMCID: PMC1523313
- DOI: 10.1063/1.1785844
Optical trapping
Abstract
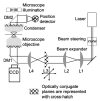
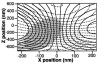
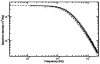
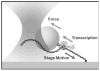
Since their invention just over 20 years ago, optical traps have emerged as a powerful tool with broad-reaching applications in biology and physics. Capabilities have evolved from simple manipulation to the application of calibrated forces on-and the measurement of nanometer-level displacements of-optically trapped objects. We review progress in the development of optical trapping apparatus, including instrument design considerations, position detection schemes and calibration techniques, with an emphasis on recent advances. We conclude with a brief summary of innovative optical trapping configurations and applications.
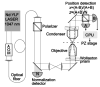
Figures









Similar articles
-
Nanophotonic trapping: precise manipulation and measurement of biomolecular arrays.Wiley Interdiscip Rev Nanomed Nanobiotechnol. 2018 Jan;10(1):10.1002/wnan.1477. doi: 10.1002/wnan.1477. Epub 2017 Apr 24. Wiley Interdiscip Rev Nanomed Nanobiotechnol. 2018. PMID: 28439980 Free PMC article. Review.
-
Optical trapping and manipulation of plasmonic nanoparticles: fundamentals, applications, and perspectives.Nanoscale. 2014 May 7;6(9):4458-74. doi: 10.1039/c3nr06617g. Nanoscale. 2014. PMID: 24664273
-
Optical trapping and binding.Rep Prog Phys. 2013 Feb;76(2):026401. doi: 10.1088/0034-4885/76/2/026401. Epub 2013 Jan 9. Rep Prog Phys. 2013. PMID: 23302540 Review.
-
Indirect optical trapping using light driven micro-rotors for reconfigurable hydrodynamic manipulation.Nat Commun. 2019 Mar 14;10(1):1215. doi: 10.1038/s41467-019-08968-7. Nat Commun. 2019. PMID: 30872572 Free PMC article.
-
High-Resolution "Fleezers": Dual-Trap Optical Tweezers Combined with Single-Molecule Fluorescence Detection.Methods Mol Biol. 2017;1486:183-256. doi: 10.1007/978-1-4939-6421-5_8. Methods Mol Biol. 2017. PMID: 27844430 Free PMC article.
Cited by
-
Integrated microfluidic device for single-cell trapping and spectroscopy.Sci Rep. 2013;3:1258. doi: 10.1038/srep01258. Epub 2013 Feb 13. Sci Rep. 2013. PMID: 23409249 Free PMC article.
-
A simple method for evaluating the trapping performance of acoustic tweezers.Appl Phys Lett. 2013 Feb 25;102(8):84102. doi: 10.1063/1.4793654. Appl Phys Lett. 2013. PMID: 23526834 Free PMC article.
-
Stokes trap for multiplexed particle manipulation and assembly using fluidics.Proc Natl Acad Sci U S A. 2016 Apr 12;113(15):3976-81. doi: 10.1073/pnas.1525162113. Epub 2016 Mar 28. Proc Natl Acad Sci U S A. 2016. PMID: 27035979 Free PMC article.
-
Single-molecule studies of viral DNA packaging.Adv Exp Med Biol. 2012;726:549-84. doi: 10.1007/978-1-4614-0980-9_24. Adv Exp Med Biol. 2012. PMID: 22297530 Free PMC article. Review.
-
Displacement Detection Decoupling in Counter-Propagating Dual-Beams Optical Tweezers with Large-Sized Particle.Sensors (Basel). 2020 Aug 31;20(17):4916. doi: 10.3390/s20174916. Sensors (Basel). 2020. PMID: 32878070 Free PMC article.
References
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

