An inversion formula for the exponential radon transform in spatial domain with variable focal-length fan-beam collimation geometry

Abstract

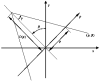
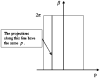
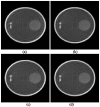
Inverting the exponential Radon transform has a potential use for SPECT (single photon emission computed tomography) imaging in cases where a uniform attenuation can be approximated, such as in brain and abdominal imaging. Tretiak and Metz derived in the frequency domain an explicit inversion formula for the exponential Radon transform in two dimensions for parallel-beam collimator geometry. Progress has been made to extend the inversion formula for fan-beam and varying focal-length fan-beam (VFF) collimator geometries. These previous fan-beam and VFF inversion formulas require a spatially variant filtering operation, which complicates the implementation and imposes a heavy computing burden. In this paper, we present an explicit inversion formula, in which a spatially invariant filter is involved. The formula is derived and implemented in the spatial domain for VFF geometry (where parallel-beam and fan-beam geometries are two special cases). Phantom simulations mimicking SPECT studies demonstrate its accuracy in reconstructing the phantom images and efficiency in computation for the considered collimator geometries.

Figure 1:

The rotated coordinate system.

Figure 2:

The VFF collimator geometry.

Figure 3:

The polar coordinates.

Figure 4.

Projections in the sinogram domain.

Figure 5:

Reconstruction results of different collimator geometries. Picture (a) is the phantom; (b) is the reconstructed image without attenuation compensation for the parallel-beam projections; (c) is the reconstructed image from the parallel-beam projections with attenuation compensation; (d) is the reconstructed image from the fan-beam projections with the focal length of D=300 pixel units; and (e) is the reconstructed image from the VFF projections with the focal length function of D(p)=100+10|p| pixel units.

Figure 6:

Reconstruction results with different focal lengths in the fan-beam geometry. Picture (a) shows the result from a focal length of D=200 pixel units; (b) of D=300 pixel units; (c) of D=400 pixel units; and (d) of D=500 pixel units.

Figure 7:

Reconstructions from projection data with Poisson noise (total counts per view is 100K). Picture (a) – fan-beam reconstructed result with D(p) =300 pixel units. Picture (b) – VFF result with D(p) = 100+10|p| pixel units. Picture (c) – profile of image (a) along the horizontal central line (where solid line is from the phantom). Picture (d) – profile of image (b) along the horizontal central line.