Metrics for external model evaluation with an application to the population pharmacokinetics of gliclazide

Abstract

Purpose: The aim of this study is to define and illustrate metrics for the external evaluation of a population model.

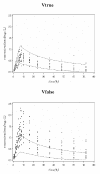
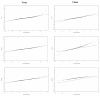
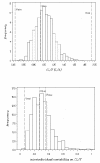
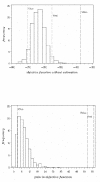
Materials and methods: In this paper, several types of metrics are defined: based on observations (standardized prediction error with or without simulation and normalized prediction distribution error); based on hyperparameters (with or without simulation); based on the likelihood of the model. All the metrics described above are applied to evaluate a model built from two phase II studies of gliclazide. A real phase I dataset and two datasets simulated with the real dataset design are used as external validation datasets to show and compare how metrics are able to detect and explain potential adequacies or inadequacies of the model.

Results: Normalized prediction errors calculated without any approximation, and metrics based on hyperparameters or on objective function have good theoretical properties to be used for external model evaluation and showed satisfactory behaviour in the simulation study.

Conclusions: For external model evaluation, prediction distribution errors are recommended when the aim is to use the model to simulate data. Metrics through hyperparameters should be preferred when the aim is to compare two populations and metrics based on the objective function are useful during the model building process.

Figure 1

Simulated concentrations versus time for V_true (top) and V_false (bottom). The dashed lines represent the 80 % predicted interval, obtained for each time-point as the 10^th and 90^th percentiles of 1000 simulations under M^B.

Figure 2

Metrics based on observations plotted versus time on V_true (left) and on V_false (right). Top: SPEY; middle: SPEYS; bottom: NPDEYS. The dashed lines represent the 95 % prediction interval for a normal distribution.

Figure 3

QQ-plots of the metrics based on observations versus the theoretical N(0,1) distribution for V_true (left) and V_false (right). The line y = x is shown to evaluate the adequacy between the theoretical and the observed distribution. Top: SPEY; middle: SPEYS; bottom: NPDEYS.

Figure 4

Histogram of the predictive distribution of simulated hyperparameters estimated using M^B: for CL/F (top) and ω²_CL/F (bottom). The values of the corresponding parameters found for V_true, V_false and V_real using an independent population analysis are shown as vertical lines.

Figure 5

Histogram of the predictive distribution of the objective function when model M^B is applied to the 1000 datasets without estimation (top) and the gain in objective function (bottom). The values of the the objective functions or of the gain found for V_true, V_false and V_real using M^B are shown as dotted lines.

Figure 6

Concentrations versus time for V_real. The dashed lines represent the 80 % predicted interval, obtained for each time-point as the 10^th and 90^th percentiles of 1000 simulations under M^B.

Figure 7

Metrics based on observations plotted versus time on V_real. Top: SPEY; middle: SPEYS; bottom: NPDEYS. The dashed lines represent the 95 % prediction interval for a normal distribution.