Mixing patterns and the spread of close-contact infectious diseases

Abstract

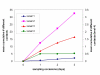
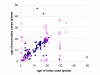
Surprisingly little is known regarding the human mixing patterns relevant to the spread of close-contact infections, such as measles, influenza and meningococcal disease. This study aims to estimate the number of partnerships that individuals make, their stability and the degree to which mixing is assortative with respect to age. We defined four levels of putative at-risk events from casual (physical contact without conversation) to intimate (contact of a sexual nature), and asked university student volunteers to record details on those they contacted at these levels on three separate days. We found that intimate contacts are stable over short time periods whereas there was no evidence of repeat casual contacts with the same individuals. The contacts were increasingly assortative as intimacy increased. Such information will aid the development and parameterisation of models of close contact diseases, and may have direct use in outbreak investigations.

Figure 1

The mean cumulative number of different individuals contacted over the three study days (sampling occasions) by contact intensity. Note that as the number of Level 4 contacts was smaller than the other types of contact they are plotted on a different scale (right-hand axis).

Figure 2

Log₁₀-log₁₀ plot of the cumulative distribution of the total number of unique contacts made at Levels 1–3 and all contacts over the three sampling days.

Figure 3

The difference in age between participants and their contacts by intensity of contact.

Figure 4

The age of primary and secondary (based on date of onset) cases of measles (open squares) and meningococcal meningitis (filled diamonds) in clusters in England and Wales 1995–1998.