Decoding stimulus variance from a distributional neural code of interspike intervals
- PMID: 16943561
- PMCID: PMC6675329
- DOI: 10.1523/JNEUROSCI.0225-06.2006
Decoding stimulus variance from a distributional neural code of interspike intervals
Abstract
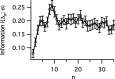
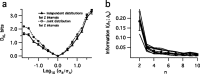
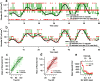
The spiking output of an individual neuron can represent information about the stimulus via mean rate, absolute spike time, and the time intervals between spikes. Here we discuss a distinct form of information representation, the local distribution of spike intervals, and show that the time-varying distribution of interspike intervals (ISIs) can represent parameters of the statistical context of stimuli. For many sensory neural systems the mapping between the stimulus input and spiking output is not fixed but, rather, depends on the statistical properties of the stimulus, potentially leading to ambiguity. We have shown previously that for the adaptive neural code of the fly H1, a motion-sensitive neuron in the fly visual system, information about the overall variance of the signal is obtainable from the ISI distribution. We now demonstrate the decoding of information about variance and show that a distributional code of ISIs can resolve ambiguities introduced by slow spike frequency adaptation. We examine the precision of this distributional code for the representation of stimulus variance in the H1 neuron as well as in the Hodgkin-Huxley model neuron. We find that the accuracy of the decoding depends on the shapes of the ISI distributions and the speed with which they adapt to new stimulus variances.
Figures



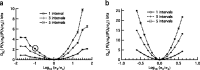

Similar articles
-
Noise, not stimulus entropy, determines neural information rate.J Comput Neurosci. 2003 Jan-Feb;14(1):23-31. doi: 10.1023/a:1021172200868. J Comput Neurosci. 2003. PMID: 12435922
-
Reproducibility and variability in neural spike trains.Science. 1997 Mar 21;275(5307):1805-8. doi: 10.1126/science.275.5307.1805. Science. 1997. PMID: 9065407
-
Spatiotemporal spike encoding of a continuous external signal.Neural Comput. 2002 Jul;14(7):1599-628. doi: 10.1162/08997660260028638. Neural Comput. 2002. PMID: 12079548
-
How the brain uses time to represent and process visual information(1).Brain Res. 2000 Dec 15;886(1-2):33-46. doi: 10.1016/s0006-8993(00)02751-7. Brain Res. 2000. PMID: 11119685 Review.
-
Adaptation in spiking neurons based on the noise shaping neural coding hypothesis.Neural Netw. 2001 Jul-Sep;14(6-7):907-19. doi: 10.1016/s0893-6080(01)00077-6. Neural Netw. 2001. PMID: 11665781 Review.
Cited by
-
Expectation violations enhance neuronal encoding of sensory information in mouse primary visual cortex.Nat Commun. 2023 Mar 2;14(1):1196. doi: 10.1038/s41467-023-36608-8. Nat Commun. 2023. PMID: 36864037 Free PMC article.
-
Temporal pairwise spike correlations fully capture single-neuron information.Nat Commun. 2016 Dec 15;7:13805. doi: 10.1038/ncomms13805. Nat Commun. 2016. PMID: 27976717 Free PMC article.
-
Neurons in the inferior colliculus use multiplexing to encode features of frequency-modulated sweeps.bioRxiv [Preprint]. 2025 Feb 10:2025.02.10.637492. doi: 10.1101/2025.02.10.637492. bioRxiv. 2025. PMID: 39990317 Free PMC article. Preprint.
-
Fractional differentiation by neocortical pyramidal neurons.Nat Neurosci. 2008 Nov;11(11):1335-42. doi: 10.1038/nn.2212. Epub 2008 Oct 19. Nat Neurosci. 2008. PMID: 18931665 Free PMC article.
-
Timescales of inference in visual adaptation.Neuron. 2009 Mar 12;61(5):750-61. doi: 10.1016/j.neuron.2009.01.019. Neuron. 2009. PMID: 19285471 Free PMC article.
References
-
- Baccus SA, Meister M. Fast and slow contrast adaptation in retinal circuitry. Neuron. 2002;36:909–919. - PubMed
-
- Bialek W, Rieke F, de Ruyter van Steveninck RR, Warland D. Reading a neural code. Science. 1991;252:1854–1857. - PubMed
-
- Brenner N, Strong SP, Koberle R, Bialek W, de Ruyter van Steveninck RR. Synergy in a neural code. Neural Comput. 2000;12:1531–1552. - PubMed
-
- Carandini M, Ferster D. A tonic hyperpolarization underlying contrast adaptation in cat visual cortex. Science. 1997;276:949–952. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
