The folding energy landscape of the dimerization domain of Escherichia coli Trp repressor: a joint experimental and theoretical investigation
- PMID: 16956620
- PMCID: PMC1866298
- DOI: 10.1016/j.jmb.2006.07.080
The folding energy landscape of the dimerization domain of Escherichia coli Trp repressor: a joint experimental and theoretical investigation
Abstract
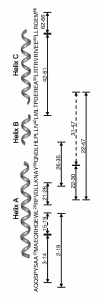
Enhanced structural insights into the folding energy landscape of the N-terminal dimerization domain of Escherichia coli tryptophan repressor, [2-66]2 TR, were obtained from a combined experimental and theoretical analysis of its equilibrium folding reaction. Previous studies have shown that the three intertwined helices in [2-66]2 TR are sufficient to drive the formation of a stable dimer for the full-length protein, [2-107]2 TR. The monomeric and dimeric folding intermediates that appear during the folding reactions of [2-66]2 TR have counterparts in the folding mechanism of the full-length protein. The equilibrium unfolding energy surface on which the folding and dimerization reactions occur for [2-66]2 TR was examined with a combination of native-state hydrogen exchange analysis, pepsin digestion and matrix-assisted laser/desorption mass spectrometry performed at several concentrations of protein and denaturant. Peptides corresponding to all three helices in [2-66]2 TR show multi-layered protection patterns consistent with the relative stabilities of the dimeric and monomeric folding intermediates. The observation of protection exceeding that offered by the dimeric intermediate in segments from all three helices implies that a segment-swapping mechanism may be operative in the monomeric intermediate. Protection greater than that expected from the global stability for a single amide hydrogen in a peptide from the C-helix possibly and another from the A-helix may reflect non-random structure, possibly a precursor for segment swapping, in the urea-denatured state. Native topology-based model simulations that correspond to a funnel energy landscape capture both the monomeric and dimeric intermediates suggested by the HX MS data and provide a rationale for the progressive acquisition of secondary structure in their conformational ensembles.
Figures






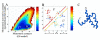



References
-
- Onuchic JN, Wolynes PG. Theory of protein folding. Curr. Opin. Struct. Biol. 2004;14:70–75. - PubMed
-
- Chavez LL, Onuchic JN, Clementi C. Quantifying the roughness on the free energy landscape: entropic bottlenecks and protein folding rates. J. Am. Chem. Soc. 2004;126:8426–8432. - PubMed
-
- Koga N, Takada S. Roles of native topology and chain-length scaling in protein folding: a simulation study with a Go-like model. J. Mol. Biol. 2001;313:171–180. - PubMed
-
- Clementi C, Nymeyer H, Onuchic JN. Topological and energetic factors: what determines the structural details of the transition state ensemble and “en-route” intermediates for protein folding? An investigation for small globular proteins. J. Mol. Biol. 2000;298:937–953. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources

