Controlled Support MEG imaging

Abstract

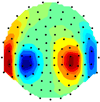
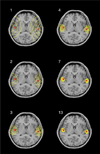
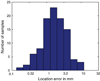
In this paper, we present a novel approach to imaging sparse and focal neural current sources from MEG (magnetoencephalography) data. Using the framework of Tikhonov regularization theory, we introduce a new stabilizer that uses the concept of controlled support to incorporate a priori assumptions about the area occupied by focal sources. The paper discusses the underlying Tikhonov theory and its relationship to a Bayesian formulation which in turn allows us to interpret and better understand other related algorithms.

Fig. 1

This Figure illustrates outcomes of two attempts to image a single focal source with two different stabilizers. (a) Image obtained with minimum support stabilizer is a cloud of disconnected multiple focal sources located near each other. (b) Image obtained with controlled support stabilizer is a single patch.

Fig. 2

Functionals S_min and S_reg are invariant to image level and discretization. For illustration, consider a 2D model depicted in this figure. Model has a non-zero domain in the middle. Left panel, shows case with 100 pixels and 4 non-zeros. Functional values for this model are S_min=0.04 and S_reg=1. Right panel, same case with finer discretization, 400 pixels and 16 non-zero values.

Fig. 3

Geometry that was used in the model study. An outer head surface was extracted from the subject's MRI. MEG sensor array (a “hat” consisting of square receiver “plates”, as shown here) was positioned in MRI coordinates by matching the reference points to the head surface. Each “plate” measures normal component of a magnetic field.

Fig. 4

Location of two test dipoles (stars) within the head.

Fig. 5

Magnetic field data for two-dipole model (the model from Fig. 4). Data are shown by color map superimposed on flat projection of measuring array (the helmet from Fig. 3). Dots show the locations of the sensors, each sensor corresponds to one plate in Fig. 3. Data contain Gaussian random noise such that the SNR=400.

Fig. 6

Evolution of stabilizers during reweighted iterations. Solid line shows evolution of S, dashes show evolution of αS_reg and dots show the evolution of (1−α)S_min. Stars show the stopping point, where term (1−α)S_min becomes less than term αS_reg. After that point term αS_reg (dashes) dominates, and S_con (solid line) flattens, as illustrated by this figure.

Fig. 7

Evolution of solution during reweighted iterations. The case corresponds to example discussed in Fig. 6. Stars show “true” location of dipoles (location of dipoles within the head is shown in Fig. 4). Solution is superimposed on corresponding MRI slice as isolines. Panels numbered 1, 2, 3, 4, 7, 13 show the solutions at the corresponding iteration.

Fig. 8

Histogram of localization errors for 100 experiments with a randomly located dipole. Average error is 2.1 mm, seven errors are above 4 mm.