Computational principles of sensorimotor control that minimize uncertainty and variability
- PMID: 17008369
- PMCID: PMC2075158
- DOI: 10.1113/jphysiol.2006.120121
Computational principles of sensorimotor control that minimize uncertainty and variability
Abstract
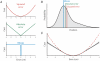
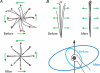
Sensory and motor noise limits the precision with which we can sense the world and act upon it. Recent research has begun to reveal computational principles by which the central nervous system reduces the sensory uncertainty and movement variability arising from this internal noise. Here we review the role of optimal estimation and sensory filtering in extracting the sensory information required for motor planning, and the role of optimal control, motor adaptation and impedance control in the specification of the motor output signal.
Figures

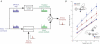
Similar articles
-
Probabilistic mechanisms in sensorimotor control.Novartis Found Symp. 2006;270:191-8; discussion 198-202, 232-7. Novartis Found Symp. 2006. PMID: 16649715 Review.
-
Computational mechanisms of sensorimotor control.Neuron. 2011 Nov 3;72(3):425-42. doi: 10.1016/j.neuron.2011.10.006. Neuron. 2011. PMID: 22078503 Review.
-
Probabilistic models in human sensorimotor control.Hum Mov Sci. 2007 Aug;26(4):511-24. doi: 10.1016/j.humov.2007.05.005. Epub 2007 Jul 12. Hum Mov Sci. 2007. PMID: 17628731 Free PMC article. Review.
-
Computational principles of movement neuroscience.Nat Neurosci. 2000 Nov;3 Suppl:1212-7. doi: 10.1038/81497. Nat Neurosci. 2000. PMID: 11127840 Review.
-
Optimality, stochasticity, and variability in motor behavior.J Comput Neurosci. 2008 Feb;24(1):57-68. doi: 10.1007/s10827-007-0041-y. Epub 2007 May 22. J Comput Neurosci. 2008. PMID: 18202922 Free PMC article.
Cited by
-
The effect of fatigue from exercise on human limb position sense.J Physiol. 2010 Apr 15;588(Pt 8):1369-77. doi: 10.1113/jphysiol.2010.187732. Epub 2010 Mar 1. J Physiol. 2010. PMID: 20194123 Free PMC article.
-
Attainment of Quiet Standing in Humans: Are the Lower Limb Joints Controlled Relative to a Misaligned Postural Reference?Front Physiol. 2019 Jun 6;10:625. doi: 10.3389/fphys.2019.00625. eCollection 2019. Front Physiol. 2019. PMID: 31275151 Free PMC article.
-
Variability in locomotor dynamics reveals the critical role of feedback in task control.Elife. 2020 Jan 23;9:e51219. doi: 10.7554/eLife.51219. Elife. 2020. PMID: 31971509 Free PMC article.
-
Exploring disturbance as a force for good in motor learning.PLoS One. 2020 May 20;15(5):e0224055. doi: 10.1371/journal.pone.0224055. eCollection 2020. PLoS One. 2020. PMID: 32433704 Free PMC article.
-
Efference Copy Is Necessary for the Attenuation of Self-Generated Touch.iScience. 2020 Feb 21;23(2):100843. doi: 10.1016/j.isci.2020.100843. Epub 2020 Jan 16. iScience. 2020. PMID: 32058957 Free PMC article.
References
-
- Albus JS. A theory of cerebellar functions. Math Biosci. 1971;10:25–61.
-
- Angel RW, Malenka RC. Velocity-dependent suppression of cutaneous sensitivity during movement. Exp Neurol. 1982;77:266–274. - PubMed
-
- Bahill AT, Clark MR, Stark L. The main sequence, a tool for studying human eye movements. Math Biosci. 1975;24:191–204.
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources

