Compliant leg behaviour explains basic dynamics of walking and running

Abstract

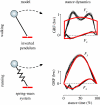
The basic mechanics of human locomotion are associated with vaulting over stiff legs in walking and rebounding on compliant legs in running. However, while rebounding legs well explain the stance dynamics of running, stiff legs cannot reproduce that of walking. With a simple bipedal spring-mass model, we show that not stiff but compliant legs are essential to obtain the basic walking mechanics; incorporating the double support as an essential part of the walking motion, the model reproduces the characteristic stance dynamics that result in the observed small vertical oscillation of the body and the observed out-of-phase changes in forward kinetic and gravitational potential energies. Exploring the parameter space of this model, we further show that it not only combines the basic dynamics of walking and running in one mechanical system, but also reveals these gaits to be just two out of the many solutions to legged locomotion offered by compliant leg behaviour and accessed by energy or speed.

Figure 1

Standard conceptual models of legged locomotion and their predictive power with respect to walking and running dynamics. The inverted pendulum and the spring–mass system are the standard models for walking and running. The model-predicted stance dynamics (red lines) fit experimental data (black traces recorded from human treadmill walking at 1.2 m s⁻¹ and running at 4.0 m s⁻¹) only for the spring–mass model for running. Note that, in the inverted pendulum dynamics, delta functions appear at 0 and 100% stance time if one adds collision and push-off models imitating double support. F_x,y, horizontal and vertical ground reaction force (GRF) normalized to body weight (bw).

Figure 2

The bipedal spring–mass model. The model has two independent, massless spring legs attached to a point mass m. Both springs have stiffness k, rest length ${\ell }_0$ and, in their swing phases, a constant orientation α₀ with respect to gravity (g, gravitational acceleration). A single step is shown that starts at the highest COM position in left leg single support (apex i), includes the double support ranging from right leg touchdown (right TD) to left leg take-off (left TO), and ends at the next apex in right leg single support (apex i+1). FP, foot point position in single support.

Figure 3

Stance-phase patterns of walking at about 1.2 m s⁻¹. (A–C) Examples of three characteristic steady-state solutions of the bipedal spring–mass model are compared with (exp) experimental results (mean and s.d. shown as line and shaded area) of five subjects (mean±s.d. of mass: 81±3.5 kg, leg length: 1.07±0.03 m) walking on a treadmill (Adal3D, TecMachine, France; with force sensors recording horizontal and vertical GRFs). The subplots show horizontal and vertical GRFs, F_x and F_y; vertical displacement, Δy; and changes in forward kinetic and gravitational potential energies, ΔE_k,x and ΔE_p. The vertical displacement is compared with that of an inverted pendulum (dashed line). The shaded segments at the time-scales denote double supports. The depicted lengths of the time-scales reflect the absolute stance times.

Figure 4

Parameter domains for stable walking and running. (a) Combinations of angle of attack α₀, spring stiffness k and system energy E_s leading to stable locomotion are shown. Related to E_s, the locomotion speed v is shown, which is the average speed of all solutions that belong to one system energy (maximum deviation 0.1 m s⁻¹ at E_s=800 J). The model finds stable walking at low energies or slow speeds (walking domains): next to the domain with double-peak patterns of the vertical GRF, domains with multi-peak patterns exist (small icons). Owing to the limited scan resolution, only domains with up to five peaks are resolved, and the four- and five-peak domains seem to overlap. Circles indicate the parameter sets of the examples A–C shown in figure 3. In addition to walking, the model finds stable running with single-peak vertical GRF above an energy or speed gap of about 500 J or 1.5 m s⁻¹ (running domain). Note the different scales of system energy at the walking domains and the running domain. (b) A slice at E_s=816 J (v∼1.2 m s⁻¹) through the walking domain with double-peak patterns is shown. Three sub-domains of parameters exist that lead to three qualitatively different steady-state patterns (small icons) exemplified by the three solutions A–C (compare figure 3).