Mathematical modeling of tumor therapy with oncolytic viruses: effects of parametric heterogeneity on cell dynamics
- PMID: 17018145
- PMCID: PMC1622743
- DOI: 10.1186/1745-6150-1-30
Mathematical modeling of tumor therapy with oncolytic viruses: effects of parametric heterogeneity on cell dynamics
Abstract
Background: One of the mechanisms that ensure cancer robustness is tumor heterogeneity, and its effects on tumor cells dynamics have to be taken into account when studying cancer progression. There is no unifying theoretical framework in mathematical modeling of carcinogenesis that would account for parametric heterogeneity.
Results: Here we formulate a modeling approach that naturally takes stock of inherent cancer cell heterogeneity and illustrate it with a model of interaction between a tumor and an oncolytic virus. We show that several phenomena that are absent in homogeneous models, such as cancer recurrence, tumor dormancy, and others, appear in heterogeneous setting. We also demonstrate that, within the applied modeling framework, to overcome the adverse effect of tumor cell heterogeneity on the outcome of cancer treatment, a heterogeneous population of an oncolytic virus must be used. Heterogeneity in parameters of the model, such as tumor cell susceptibility to virus infection and the ability of an oncolytic virus to infect tumor cells, can lead to complex, irregular evolution of the tumor. Thus, quasi-chaotic behavior of the tumor-virus system can be caused not only by random perturbations but also by the heterogeneity of the tumor and the virus.
Conclusion: The modeling approach described here reveals the importance of tumor cell and virus heterogeneity for the outcome of cancer therapy. It should be straightforward to apply these techniques to mathematical modeling of other types of anticancer therapy.
Reviewers: Leonid Hanin (nominated by Arcady Mushegian), Natalia Komarova (nominated by Orly Alter), and David Krakauer.
Figures
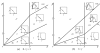
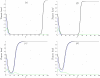
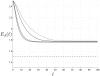

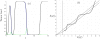

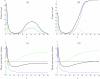
References
-
- Alexandrova R. Tumour heterogeneity. Exper Path and Paras. 2001;4:57–67.
LinkOut - more resources
Full Text Sources

