Penalized weighted least-squares approach to sinogram noise reduction and image reconstruction for low-dose X-ray computed tomography
- PMID: 17024831
- PMCID: PMC1619874
- DOI: 10.1109/42.896783
Penalized weighted least-squares approach to sinogram noise reduction and image reconstruction for low-dose X-ray computed tomography
Abstract
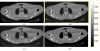
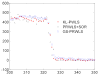
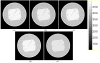
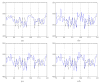
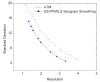
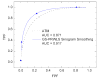
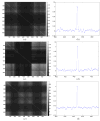
Reconstructing low-dose X-ray computed tomography (CT) images is a noise problem. This work investigated a penalized weighted least-squares (PWLS) approach to address this problem in two dimensions, where the WLS considers first- and second-order noise moments and the penalty models signal spatial correlations. Three different implementations were studied for the PWLS minimization. One utilizes a Markov random field (MRF) Gibbs functional to consider spatial correlations among nearby detector bins and projection views in sinogram space and minimizes the PWLS cost function by iterative Gauss-Seidel algorithm. Another employs Karhunen-Loève (KL) transform to de-correlate data signals among nearby views and minimizes the PWLS adaptively to each KL component by analytical calculation, where the spatial correlation among nearby bins is modeled by the same Gibbs functional. The third one models the spatial correlations among image pixels in image domain also by a MRF Gibbs functional and minimizes the PWLS by iterative successive over-relaxation algorithm. In these three implementations, a quadratic functional regularization was chosen for the MRF model. Phantom experiments showed a comparable performance of these three PWLS-based methods in terms of suppressing noise-induced streak artifacts and preserving resolution in the reconstructed images. Computer simulations concurred with the phantom experiments in terms of noise-resolution tradeoff and detectability in low contrast environment. The KL-PWLS implementation may have the advantage in terms of computation for high-resolution dynamic low-dose CT imaging.
Figures
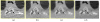



References
-
- Linton OW, Fred A, Mettler FA. “National conference on dose reduction in CT, with an emphasis on pediatric patients”. American Journal of Roentgenology. 2003;181:321–329. - PubMed
-
- Lange K, Carson R. “EM reconstruction algorithms for emission and transmission tomography”. J Computer Assisted Tomography. 1984;8:306–316. - PubMed
-
- Elbakri IA, Fessler JA. “Efficient and accurate likelihood for iterative image reconstruction in X-ray computed tomography”. Proc SPIE Med Imaging. 2003;5032:1839–1850.
-
- Lu H, Li X, Hsiao IT, Liang Z. “Analytical noise treatment for low-dose CT projection data by penalized weighted least-squares smoothing in the K-L domain”. Proc SPIE Med Imaging. 2002;4682:146–152.
-
- Li T, Li X, Wang J, Wen J, Lu H, Hsieh J, Liang Z. “Nonlinear sinogram smoothing for low-dose X-ray CT”. IEEE Trans Nucl Science. 2004;51:2505–2513.
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Medical
Miscellaneous

