Characterization of the nanoscale properties of individual amyloid fibrils

Abstract

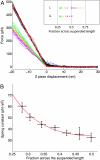
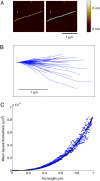
We report the detailed mechanical characterization of individual amyloid fibrils by atomic force microscopy and spectroscopy. These self-assembling materials, formed here from the protein insulin, were shown to have a strength of 0.6 +/- 0.4 GPa, comparable to that of steel (0.6-1.8 GPa), and a mechanical stiffness, as measured by Young's modulus, of 3.3 +/- 0.4 GPa, comparable to that of silk (1-10 GPa). The values of these parameters reveal that the fibrils possess properties that make these structures highly attractive for future technological applications. In addition, analysis of the solution-state growth kinetics indicated a breakage rate constant of 1.7 +/- 1.3 x 10(-8) s(-1), which reveals that a fibril 10 mum in length breaks spontaneously on average every 47 min, suggesting that internal fracturing is likely to be of fundamental importance in the proliferation of amyloid fibrils and therefore for understanding the progression of their associated pathogenic disorders.

Fig. 1.

Mechanical manipulation of a two-filament insulin fibril with the atomic force microscope. (A) Insulin amyloid fibrils were deposited onto a patterned gold surface, and contact mode AFM topographic images were obtained in aqueous 0.01 M HCl (image size 400 nm, z scale 30 nm). (B) Force spectroscopy was subsequently performed on the suspended fibril and a characteristic force-distance curve with four identifiable regions was obtained ([1] noncontact, [2] linear elastic, [3] nonlinear, [4] surface). The serial cantilever-fibril spring constant k_s was determined by a linear least-squares fit (green line, slope = −19.3 pN/nm) in the linear elastic region, and in the nonlinear region the slope of the force-distance curve (red line, slope = −25.3 pN/nm) is the cantilever spring constant. Breakage of amyloid fibrils was observed in additional force-distance curves (Inset), and the maximal breakage force F_max for each was determined. (C) To confirm breakage an additional contact mode AFM topographic image was acquired (image size 400 nm, z scale 30 nm) with identical scan parameters to the image acquired in A.

Fig. 2.

Determination of the bending rigidity of two-filament insulin fibrils from mechanical manipulation in the atomic force microscope. (A) Force-distance curves were acquired on 21 independent samples of two-filament insulin fibrils, corresponding to >2,000 measurements of deflection at a given force (colored curves). The position at which the force was applied was recorded, and the dimensionless fraction across the suspended length was calculated (i, Inset, and normalized between 0 and 0.5, ii, Inset). The corresponding force-distance curve and fraction across the suspended length have been assigned matching colors. Additionally, force-distance curves were acquired on the surface (black curves), and the average of 10 independent measurements is shown (red curve, k_c = 23.6 pN/nm). The spring constant of a fibril k was calculated as k = k_ck_s/(k_c − k_s). (B) For each of the force-distance curves in A the fibril spring constant and fraction across the suspended length was calculated on two-filament fibrils suspended 75.3 ± 2.6 nm. The average (points) and range (error bars) of the fibril spring constant per bin are plotted as a function of the fraction across the suspended length f and best-fit to the linear elastic prediction with Young's and shape adjusted shear moduli (G/ξ) of 3.3 and 0.28 GPa, respectively (red curve).

Fig. 3.

Measurement of the bending rigidity of fibrils by analysis of thermal fluctuations. (A and B) The shape of the fibrils was automatically extracted from the AFM height data (A Left) by using a tracing algorithm (A Right) and secants (see Materials and Methods) on 76 fibrils were analyzed (contours shown in B). (C) The midpoint mean square fluctuations as a function of the secant length with data in 1,000 bins and a one parameter fit to the cubic equation predicted by the linear elastic model (see Materials and Methods). The fit gives a value of C_B = 1.7 × 10⁻²⁵ ± 1.2 × 10⁻²⁶ N·m² for the bending rigidity of the structures.

Fig. 4.

Breakage of amyloid fibrils. (A) A proposed mechanism of amyloid fibril formation involves nucleation (row 1), elongation (row 2), dissociation (row 3), and breakage (row 4). The breakage rate constant was determined from seeded growth experiments. (B) For each of 10 independent seeded growth experiments with different initial monomer concentration, the average length as a function of time was monitored by dynamic light scattering (Inset). (C) The values of L₀ and (dL/dt)|_t=0 were calculated. A linear least-squares fit (red line, slope = 3.6 × 10⁵ M⁻¹·s⁻¹, intercept = −0.54 s⁻¹) was performed on the data. With an average initial length L₀ = 1,361 nm, equivalent to 11,340 monomers, the values of the slope and intercept imply an elongation rate constant of 1.8 ± 0.2 × 10⁵ M⁻¹·s⁻¹ and breakage rate constant of 1.7 ± 1.3 × 10⁻⁸ s⁻¹. Preformed, sonicated insulin fibrils (50 nM) in a solution of insulin (1 μM) were heated at 60°C, and the average length of two-filament insulin fibrils as a function of time was measured with the AFM (points). The differential equations for the nucleated growth model with breakage were solved numerically (shaded region) with the initial conditions of the experiment and the elongation rate constant was determined. The breakage rate constant was varied between the upper and lower bound of that determined. The dashed curve shows the numerical solution to the differential equations in the absence of breakage.