Evaluation of regression models in metabolic physiology: predicting fluxes from isotopic data without knowledge of the pathway

Abstract

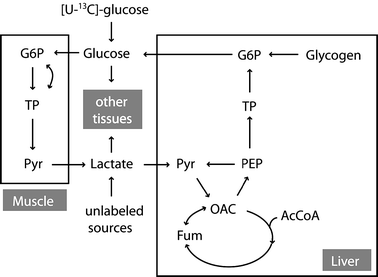
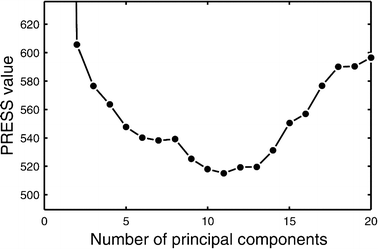
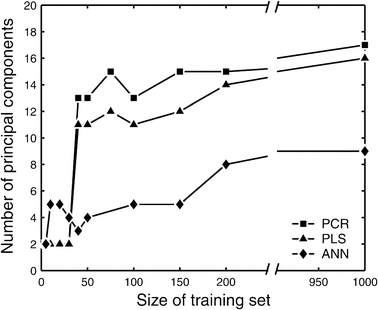
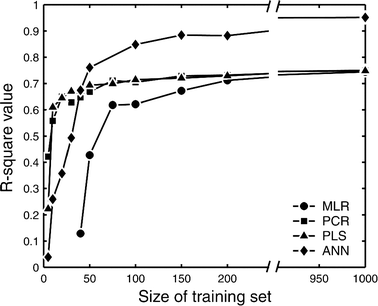
This study explores the ability of regression models, with no knowledge of the underlying physiology, to estimate physiological parameters relevant for metabolism and endocrinology. Four regression models were compared: multiple linear regression (MLR), principal component regression (PCR), partial least-squares regression (PLS) and regression using artificial neural networks (ANN). The pathway of mammalian gluconeogenesis was analyzed using [U-(13)C]glucose as tracer. A set of data was simulated by randomly selecting physiologically appropriate metabolic fluxes for the 9 steps of this pathway as independent variables. The isotope labeling patterns of key intermediates in the pathway were then calculated for each set of fluxes, yielding 29 dependent variables. Two thousand sets were created, allowing independent training and test data. Regression models were asked to predict the nine fluxes, given only the 29 isotopomers. For large training sets (>50) the artificial neural network model was superior, capturing 95% of the variability in the gluconeogenic flux, whereas the three linear models captured only 75%. This reflects the ability of neural networks to capture the inherent non-linearities of the metabolic system. The effect of error in the variables and the addition of random variables to the data set was considered. Model sensitivities were used to find the isotopomers that most influenced the predicted flux values. These studies provide the first test of multivariate regression models for the analysis of isotopomer flux data. They provide insight for metabolomics and the future of isotopic tracers in metabolic research where the underlying physiology is complex or unknown.

Figure 1.

Schematic representation of mammalian glucose metabolism evaluated by constant [U−¹³C]glucose infusion. Abbreviations of metabolites: G6P, glucose-6-phosphate; Pyr, pyruvate; OAC, oxaloacetate; Fum, fumarate; AcCoA, acetyl coenzyme A; PEP, phosphoenolpyruvate; TP, triose phosphates.

Figure 2.

Determination of the optimal number of principal components by the leave-one-out cross-validation method. The optimal number of principal components is defined as the fewest number of components yielding a PRESS value within 5% of the minimal observed PRESS value; in this case 10 principal components.

Figure 3.

Optimal number of principal components in the PCR and PLS models for varying sizes of training data set. Larger training sets allow more principal components to be included in the model to capture the finer details of the system. ANN models typically required fewer principal components than PCR and PLS models.

Figure 4.

Observed prediction accuracy of the gluconeogenesis flux as a function of the number of samples used in training. For small number of training samples the PCR and PLS models produce the best predictions; for larger number of training samples ANN yields the best predictions.