Desensitization contributes to the synaptic response of gain-of-function mutants of the muscle nicotinic receptor
- PMID: 17074980
- PMCID: PMC2151585
- DOI: 10.1085/jgp.200609570
Desensitization contributes to the synaptic response of gain-of-function mutants of the muscle nicotinic receptor
Abstract
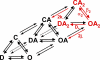
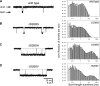
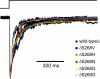
Although the muscle nicotinic receptor (AChR) desensitizes almost completely in the steady presence of high concentrations of acetylcholine (ACh), it is well established that AChRs do not accumulate in desensitized states under normal physiological conditions of neurotransmitter release and clearance. Quantitative considerations in the framework of plausible kinetic schemes, however, lead us to predict that mutations that speed up channel opening, slow down channel closure, and/or slow down the dissociation of neurotransmitter (i.e., gain-of-function mutations) increase the extent to which AChRs desensitize upon ACh removal. In this paper, we confirm this prediction by applying high-frequency trains of brief ( approximately 1 ms) ACh pulses to outside-out membrane patches expressing either lab-engineered or naturally occurring (disease-causing) gain-of-function mutants. Entry into desensitization was evident in our experiments as a frequency-dependent depression in the peak value of succesive macroscopic current responses, in a manner that is remarkably consistent with the theoretical expectation. We conclude that the comparatively small depression of the macroscopic currents observed upon repetitive stimulation of the wild-type AChR is due, not to desensitization being exceedingly slow but, rather, to the particular balance between gating, entry into desensitization, and ACh dissociation rate constants. Disruption of this fine balance by, for example, mutations can lead to enhanced desensitization even if the kinetics of entry into, and recovery from, desensitization themselves are not affected. It follows that accounting for the (usually overlooked) desensitization phenomenon is essential for the correct interpretation of mutagenesis-driven structure-function relationships and for the understanding of pathological synaptic transmission at the vertebrate neuromuscular junction.
Figures
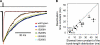






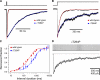
References
-
- Barbour, B., and M. Häusser. 1997. Intersynaptic diffusion of neurotransmitter. Trends Neurosci. 20:377–384. - PubMed
-
- Chen, C., D.M. Blitz, and W.G. Regehr. 2002. Contributions of receptor desensitization and saturation to plasticity at the retinogeniculate synapse. Neuron. 33:779–788. - PubMed
-
- Colquhoun, D., and A.G. Hawkes. 1982. On the stochastic properties of bursts of single ion channel openings and of clusters of bursts. Philos. Trans. R. Soc. Lond. B Biol. Sci. 300:1–89. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Miscellaneous

