Analysis of squat and stoop dynamic liftings: muscle forces and internal spinal loads

Abstract

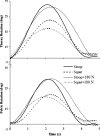
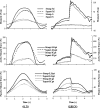
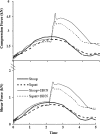
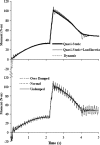
Despite the well-recognized role of lifting in back injuries, the relative biomechanical merits of squat versus stoop lifting remain controversial. In vivo kinematics measurements and model studies are combined to estimate trunk muscle forces and internal spinal loads under dynamic squat and stoop lifts with and without load in hands. Measurements were performed on healthy subjects to collect segmental rotations during lifts needed as input data in subsequent model studies. The model accounted for nonlinear properties of the ligamentous spine, wrapping of thoracic extensor muscles to take curved paths in flexion and trunk dynamic characteristics (inertia and damping) while subject to measured kinematics and gravity/external loads. A dynamic kinematics-driven approach was employed accounting for the spinal synergy by simultaneous consideration of passive structures and muscle forces under given posture and loads. Results satisfied kinematics and dynamic equilibrium conditions at all levels and directions. Net moments, muscle forces at different levels, passive (muscle or ligamentous) forces and internal compression/shear forces were larger in stoop lifts than in squat ones. These were due to significantly larger thorax, lumbar and pelvis rotations in stoop lifts. For the relatively slow lifting tasks performed in this study with the lowering and lifting phases each lasting approximately 2 s, the effect of inertia and damping was not, in general, important. Moreover, posterior shift in the position of the external load in stoop lift reaching the same lever arm with respect to the S1 as that in squat lift did not influence the conclusion of this study on the merits of squat lifts over stoop ones. Results, for the tasks considered, advocate squat lifting over stoop lifting as the technique of choice in reducing net moments, muscle forces and internal spinal loads (i.e., moment, compression and shear force).

Fig. 1

Representation of the model as well as global and local musculatures in the sagittal and frontal planes. Fascicles on one side are shown; ICpl iliocostalis lumborum pars lumborum, ICpt iliocostalis lumborum pars thoracic, IP iliopsoas, LGpl longissimus thoracis pars lumborum, LGpt longissimus thoracis pars thoracic, MF multifidus, QL quadratus lumborum, IO internal oblique, EO external oblique and RA rectus abdominus

Fig. 2

Prescribed thorax (top) and pelvis (bottom) rotations in the model for various cases based on in vivo measurements of a typical subject (smoothed by 6th order polynomials, R² > 98%). The T12–S1 rotations are subsequently prescribed in the model based on the difference between these two rotations and proportions given in the text

Fig. 3

Predicted temporal variation of sagittal moments at the L5–S1 level for different cases (N m); net external moment (top), portion resisted by muscle forces (middle) and portion resisted by passive ligamentous spine (bottom). For the cases with load in hands, the sharp increase in moments is noted as the load reaches its maximum value of 180  N in 0.2 s duration

Fig. 4

Predicted temporal variation of net external moment at the T12 level (top) and associated active (middle) and passive (bottom) global muscle (LGpt longissimus and ICpt illiocostalis) forces for different lifting techniques without any load in hands (left side) and 180 N load in hands (right side). The rising time of 180 N external load applied in hands is shown by lines on the right. S moment resisted by passive spine, M moment resisted by muscles

Fig. 5

Maximum predicted total local and global muscle forces at various levels for different cases

Fig. 6

Computed temporal variation of local compression (top) and anterior shear (bottom) forces at the L5–S1 level for different cases. These forces are normal and tangential to the disc mid-height planes

Fig. 7

Predicted effect of changes in system dynamics characteristics on the net moment at the T12 level for the squat lift with 180 N in hands; effect of consideration of trunk and load inertias (top) and of damping (bottom)

Fig. 8

Deformed configurations of the model at the beginning of lifting phase (i.e., end of lowering phase) for various cases. The position of the external load held in hands, also shown, has identical horizontal lever arms with respect to the T12 in both squat and stoop configurations. The deformed configurations have been shifted in both horizontal and vertical directions to place the S1 at the origin of axes. The thorax rotation is much larger in stoop lifts (70° and 66.9° without and with load, respectively) than in squat lifts (49.7° and 38.4°)