A modified algorithm for the improvement of composite interval mapping
- PMID: 17110476
- PMCID: PMC1775001
- DOI: 10.1534/genetics.106.066811
A modified algorithm for the improvement of composite interval mapping
Abstract
Composite interval mapping (CIM) is the most commonly used method for mapping quantitative trait loci (QTL) with populations derived from biparental crosses. However, the algorithm implemented in the popular QTL Cartographer software may not completely ensure all its advantageous properties. In addition, different background marker selection methods may give very different mapping results, and the nature of the preferred method is not clear. A modified algorithm called inclusive composite interval mapping (ICIM) is proposed in this article. In ICIM, marker selection is conducted only once through stepwise regression by considering all marker information simultaneously, and the phenotypic values are then adjusted by all markers retained in the regression equation except the two markers flanking the current mapping interval. The adjusted phenotypic values are finally used in interval mapping (IM). The modified algorithm has a simpler form than that used in CIM, but a faster convergence speed. ICIM retains all advantages of CIM over IM and avoids the possible increase of sampling variance and the complicated background marker selection process in CIM. Extensive simulations using two genomes and various genetic models indicated that ICIM has increased detection power, a reduced false detection rate, and less biased estimates of QTL effects.
Figures


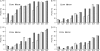


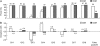

References
-
- Dempster, A., N. Laird and D. Rubin, 1977. Maximum likelihood from incomplete data via the EM algorithm. J. R. Stat. Soc. B 39: 1–38.
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources

