Optimal noise filtering in the chemotactic response of Escherichia coli
- PMID: 17112312
- PMCID: PMC1636674
- DOI: 10.1371/journal.pcbi.0020154
Optimal noise filtering in the chemotactic response of Escherichia coli
Abstract
Information-carrying signals in the real world are often obscured by noise. A challenge for any system is to filter the signal from the corrupting noise. This task is particularly acute for the signal transduction network that mediates bacterial chemotaxis, because the signals are subtle, the noise arising from stochastic fluctuations is substantial, and the system is effectively acting as a differentiator which amplifies noise. Here, we investigated the filtering properties of this biological system. Through simulation, we first show that the cutoff frequency has a dramatic effect on the chemotactic efficiency of the cell. Then, using a mathematical model to describe the signal, noise, and system, we formulated and solved an optimal filtering problem to determine the cutoff frequency that bests separates the low-frequency signal from the high-frequency noise. There was good agreement between the theory, simulations, and published experimental data. Finally, we propose that an elegant implementation of the optimal filter in combination with a differentiator can be achieved via an integral control system. This paper furnishes a simple quantitative framework for interpreting many of the key notions about bacterial chemotaxis, and, more generally, it highlights the constraints on biological systems imposed by noise.
Conflict of interest statement
Figures



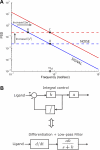
 (Protocol S1). Graphically, this is determined by the intersection of the signal and noise PSDs (point A). Increasing the noise variance (red dashed line) decreases the optimal cutoff frequency because the filter must become more restrictive to eliminate the additional noise (point B). If the signal PSD is then increased (red solid line), for example, by increasing the effect of rotational diffusion, the cutoff frequency increases (point C). Parameters used for point A: u = 20 μm/s, Dr = 0.16 rad2/s, τ = 1 s, RT = 2.5 μM, k
−/k
+ = 100 μM, g = 0.03 μM/μm, and binding is assumed at steady state with a ligand value of L
0 = 1 μM. (B) Block diagram representation of the chemotactic system. A system using an integral control feedback mechanism (top) is functionally equivalent to one consisting of the series connection of a differentiator and a first-order low-pass filter. In the chemotaxis pathway, this subsystem is followed by a conversion function of CheYp to the running bias.
(Protocol S1). Graphically, this is determined by the intersection of the signal and noise PSDs (point A). Increasing the noise variance (red dashed line) decreases the optimal cutoff frequency because the filter must become more restrictive to eliminate the additional noise (point B). If the signal PSD is then increased (red solid line), for example, by increasing the effect of rotational diffusion, the cutoff frequency increases (point C). Parameters used for point A: u = 20 μm/s, Dr = 0.16 rad2/s, τ = 1 s, RT = 2.5 μM, k
−/k
+ = 100 μM, g = 0.03 μM/μm, and binding is assumed at steady state with a ligand value of L
0 = 1 μM. (B) Block diagram representation of the chemotactic system. A system using an integral control feedback mechanism (top) is functionally equivalent to one consisting of the series connection of a differentiator and a first-order low-pass filter. In the chemotaxis pathway, this subsystem is followed by a conversion function of CheYp to the running bias.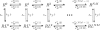

References
-
- Csete ME, Doyle JC. Reverse engineering of biological complexity. Science. 2002;295:1664–1669. - PubMed
-
- Kitano H. Computational systems biology. Nature. 2002;420:206–210. - PubMed
-
- Rao CV, Wolf DM, Arkin AP. Control, exploitation and tolerance of intracellular noise. Nature. 2002;420:231–237. - PubMed
-
- Orrell D, Bolouri H. Control of internal and external noise in genetic regulatory networks. J Theor Biol. 2004;230:301–312. - PubMed
-
- Korobkova E, Emonet T, Vilar JMG, Shimizu TS, Cluzel P. From molecular noise to behavioural variability in a single bacterium. Nature. 2004;428:574–578. - PubMed

