Support vector machine implementations for classification & clustering
- PMID: 17118147
- PMCID: PMC1683575
- DOI: 10.1186/1471-2105-7-S2-S4
Support vector machine implementations for classification & clustering
Abstract
Background: We describe Support Vector Machine (SVM) applications to classification and clustering of channel current data. SVMs are variational-calculus based methods that are constrained to have structural risk minimization (SRM), i.e., they provide noise tolerant solutions for pattern recognition. The SVM approach encapsulates a significant amount of model-fitting information in the choice of its kernel. In work thus far, novel, information-theoretic, kernels have been successfully employed for notably better performance over standard kernels. Currently there are two approaches for implementing multiclass SVMs. One is called external multi-class that arranges several binary classifiers as a decision tree such that they perform a single-class decision making function, with each leaf corresponding to a unique class. The second approach, namely internal-multiclass, involves solving a single optimization problem corresponding to the entire data set (with multiple hyperplanes).
Results: Each SVM approach encapsulates a significant amount of model-fitting information in its choice of kernel. In work thus far, novel, information-theoretic, kernels were successfully employed for notably better performance over standard kernels. Two SVM approaches to multiclass discrimination are described: (1) internal multiclass (with a single optimization), and (2) external multiclass (using an optimized decision tree). We describe benefits of the internal-SVM approach, along with further refinements to the internal-multiclass SVM algorithms that offer significant improvement in training time without sacrificing accuracy. In situations where the data isn't clearly separable, making for poor discrimination, signal clustering is used to provide robust and useful information--to this end, novel, SVM-based clustering methods are also described. As with the classification, there are Internal and External SVM Clustering algorithms, both of which are briefly described.
Figures


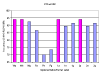
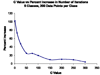

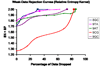




References
-
- Vapnik VN. The Nature of Statistical Learning Theory. 2. Springer-Verlag, New York; 1998.
-
- Burges CJC. A tutorial on support vector machines for pattern recognition. Data Min Knowl Discov. 1998;2:121–67.
-
- Platt JC. Fast Training of Support Vector Machines using Sequential Minimal Optimization. In: Scholkopf B, Burges CJC, Smola AJ, editor. Advances in Kernel Methods – Support Vector Learning. Ch. 12. MIT Press, Cambridge, USA; 1998.
-
- Osuna E, Freund R, Girosi. F. An improved training algorithm for support vector machines. In: Principe J, Gile L, Morgan N, and Wilson E, editor. Neural Networks for Signal Processing VII. IEEE, New York; 1997. pp. 276–85.
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Research Materials

