Community response to enrichment is highly sensitive to model structure

Abstract

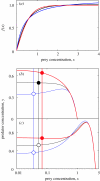
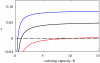
Biologists use mathematical functions to model, understand and predict nature. For most biological processes, however, the exact analytical form is not known. This is also true for one of the most basic life processes: the uptake of food or resources. We show that the use of several nearly indistinguishable functions, which can serve as phenomenological descriptors of resource uptake, may lead to alarmingly different dynamical behaviour in a simple community model. More specifically, we demonstrate that the degree of resource enrichment needed to destabilize the community dynamics depends critically on the mathematical nature of the uptake function.

Figure 1

Response to enrichment in the R–M model. (a) Three nearly congruent resource uptake curves (see table 1 for equations): black, Ivlev (f_I); blue, Holling (f_H); red, trigonometric (f_T). Nonlinear least-squares fits to Ivlev's response with a_I=1, b_I=2. (Holling: a_H=3.05, b_H=2.68; trigonometric: a_T=0.99, b_T=1.48.) (b,c) Isoclines for two levels of enrichment of the prey population in the predator–prey phase plane: (b) K=1, (c) K=4. Filled and open circles mark stable and unstable equilibria, respectively. Other parameters: r=1, m=0.1 (per time unit). Colours as in (a).

Figure 2

Stability analysis. Real part, τ, of the eigenvalue of the community matrix versus the carrying capacity, K, for different uptake curves. Positive values of τ indicate an unstable equilibrium. Although the system with f_H (blue) is far from the stability boundary at large K, a subtle change in model structure (to f_T; red) may stabilize the equilibrium. Other parameters and colours as in figure 1.