Order N algorithm for computation of electrostatic interactions in biomolecular systems

Abstract

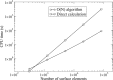
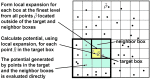
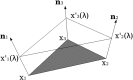
Poisson-Boltzmann electrostatics is a well established model in biophysics; however, its application to large-scale biomolecular processes such as protein-protein encounter is still limited by the efficiency and memory constraints of existing numerical techniques. In this article, we present an efficient and accurate scheme that incorporates recently developed numerical techniques to enhance our computational ability. In particular, a boundary integral equation approach is applied to discretize the linearized Poisson-Boltzmann equation; the resulting integral formulas are well conditioned and are extended to systems with arbitrary numbers of biomolecules. The solution process is accelerated by Krylov subspace methods and a new version of the fast multipole method. In addition to the electrostatic energy, fast calculations of the forces and torques are made possible by using an interpolation procedure. Numerical experiments show that the implemented algorithm is asymptotically optimal O(N) in both CPU time and required memory, and application to the acetylcholinesterase-fasciculin complex is illustrated.

Fig. 1.

Log–log plot of CPU time vs. the number of elements for the calculation on a sphere case.

Fig. 2.

Electrostatics of AChE–Fas2. (a) Surface potential map of AChE and Fas2 at separation of 14 Å. The two green arrows indicated as F and M show the force (0.10, −0.03, −0.69) and torque (−0.35, −1.03, −2.8), respectively, which are scaled for visualization. (b) The interaction energy profiles as functions of separations along a predefined unbinding direction. U, total electrostatic interaction; U₀, electrostatic interaction energy without consideration of the ligand polarization and desolvation effects as the typical treatment in UHBD; U_d-AChE and U_d-Fas2, electrostatic desolvation energies due to AChE and Fas2 cavities, respectively; U_nonpolar, nonpolar contribution from a simple surface term. (c) The x, y, z components of forces, and torques acting on Fas2 as functions of the separation distances along a predefined unbinding direction.

Fig. 3.

Schematic showing the source points ρ⇀ and evaluation point R⇀ in the new version FMM. In BEM implementation, the source points are centered at the surface triangular elements.

Fig. 4.

The prism constructed on a triangular element. The shadowed triangle is one of the boundary elements, n₁, n₂, and n₃ are three unit normal vectors at the three nodes, and λ is a parameter to describe the third-dimensional position of the prism.