"Proton holes" in long-range proton transfer reactions in solution and enzymes: A theoretical analysis

Abstract

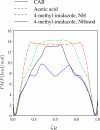
Proton transfers are fundamental to chemical processes in solution and biological systems. Often, the well-known Grotthuss mechanism is assumed where a series of sequential "proton hops" initiates from the donor and combines to produce the net transfer of a positive charge over a long distance. Although direct experimental evidence for the sequential proton hopping has been obtained recently, alternative mechanisms may be possible in complex molecular systems. To understand these events, all accessible protonation states of the mediating groups should be considered. This is exemplified by transfers through water where the individual water molecules can exist in three protonation states (water, hydronium, and hydroxide); as a result, an alternative to the Grotthuss mechanism for a proton transfer through water is to generate a hydroxide by first protonating the acceptor and then transfer the hydroxide toward the donor through water. The latter mechanism can be most generally described as the transfer of a "proton hole" from the acceptor to the donor where the "hole" characterizes the deprotonated state of any mediating molecule. This pathway is distinct and is rarely considered in the discussion of proton-transfer processes. Using a calibrated quantum mechanical/molecular mechanical (QM/MM) model and an effective sampling technique, we study proton transfers in two solution systems and in Carbonic Anhydrase II. Although the relative weight of the "proton hole" and Grotthuss mechanisms in a specific system is difficult to determine precisely using any computational approach, the current study establishes an energetics motivated framework that hinges on the donor/acceptor pKa values and electrostatics due to the environment to argue that the "proton hole" transfer is likely as important as the classical Grotthuss mechanism for proton transport in many complex molecular systems.

FIG. 1

The molecular mechanism for the proton transfer between two molecules in solution depends critically on their pK_a values and electrostatics in the environment. (a) The classical Grotthuss mechanism that involves sequential proton hops from the donor to the acceptor; (b) the hydroxide mediated mechanism that involves first protonating the acceptor and then a series of “proton hole” transfers towards the donor; (c) the relative energetics of the Grotthus and “proton hole” transfer mechanisms can be approximately estimated based on the pK_a values of the donor/acceptor groups (AH, BH) and water (W) as well as hydronium (WH⁺). With the right pK_a combinations, (e.g., when both AH and BH have pK_a larger than 7), the “proton hole” transfer pathway can be energetically more favorable than the classical Grotthuss mechanism.

FIG. 2

The “excess coordination” for the donor atom, acceptor atom and oxygen atoms in the mediating water molecules during the proton transfer reactions. Each positive/negative peak in the plot corresponds to a protonated/deprotonated heavy atom in the course of the reaction. The plots are for proton transfers between (a) two acetic acids (one protonated, one deprotonated) in solution; (b) two 4-methyl-imidazole molecules (one protonated, one charge neutral) in solution with the modified (NHmod) nitrogen-hydrogen repulsive potential in SCC-DFTB; simulations with the standard nitrogen-hydrogen repulsive potential produce results very similar to (a) and are not shown (see text for discussions); (c) zinc-bound water and His 64 in the carbonic anhydrase II when His 64 adopts the “in” configuration.

FIG. 3

Calculated potential of mean force for the various proton transfer reactions in solution and CAII based on SCC-DFTB/MM simulations; the “NH” and “NHmod” refer to the two sets of repulsive potential between nitrogen and hydrogen atoms in SCC-DFTB. The reaction coordinate is a collective coordinate that describes the progress of the proton transfer. For details, see Systems and Simulation Methods.

FIG. 4

Radial distribution functions for the solvent oxygen around the “proton hole” for the proton transfer reaction, between (a) two 4-methyl-imidazoles in solution and (b) the zinc-bound water and His 64 in CA II, at different stages in the process. The position of the “proton hole” is given by an expression similar to that for $\underset{\xi }{\to }$ in Eq.1, with the opposite sign and weights of the donor and accepter defined as the number of protons in the most protonated state relative the the reactant and product (i.e., 2 for the zinc-bound water and 1 for Nδ in His 64). In the enzyme calculations, the oxygen from Thr 200 is also included in the list of “solvent” oxygen atoms that may coordinate the “proton hole”.

FIG. 5

Snapshot and electrostatic potentials of the carbonic anhydrase II active site. (a) A snapshot from the SCC-DFTB/MM umbrella sampling simulation that illustrates the hydrogen bonding interactions that stabilize the hydroxide; the chain of water molecules that mediate the “proton hole” transfer are colored purple. (b-d) Calculated electrostatic potentials in the plane formed by the zinc ion, oxygen in the zinc-bound water and N_δ in His 64; the zinc ion is placed in the origin. The three plots are generated with different combinations of the protonation states of the zinc-bound water and His 64. (b) Zn²⁺·H₂O/His64; (c) Zn²⁺·OH⁻/His64; (d) Zn²⁺·H₂O/His64H⁺. Note that no other explicit water molecules are included in the Possion-Boltzmann calculations for the electrostatic potentials.