A method for estimation of elasticities in metabolic networks using steady state and dynamic metabolomics data and linlog kinetics
- PMID: 17184531
- PMCID: PMC1781081
- DOI: 10.1186/1471-2105-7-540
A method for estimation of elasticities in metabolic networks using steady state and dynamic metabolomics data and linlog kinetics
Abstract
Background: Dynamic modeling of metabolic reaction networks under in vivo conditions is a crucial step in order to obtain a better understanding of the (dis)functioning of living cells. So far dynamic metabolic models generally have been based on mechanistic rate equations which often contain so many parameters that their identifiability from experimental data forms a serious problem. Recently, approximative rate equations, based on the linear logarithmic (linlog) format have been proposed as a suitable alternative with fewer parameters.
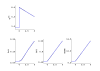
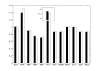
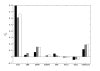
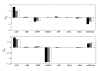
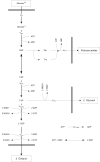
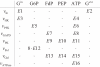
Results: In this paper we present a method for estimation of the kinetic model parameters, which are equal to the elasticities defined in Metabolic Control Analysis, from metabolite data obtained from dynamic as well as steady state perturbations, using the linlog kinetic format. Additionally, we address the question of parameter identifiability from dynamic perturbation data in the presence of noise. The method is illustrated using metabolite data generated with a dynamic model of the glycolytic pathway of Saccharomyces cerevisiae based on mechanistic rate equations. Elasticities are estimated from the generated data, which define the complete linlog kinetic model of the glycolysis. The effect of data noise on the accuracy of the estimated elasticities is presented. Finally, identifiable subset of parameters is determined using information on the standard deviations of the estimated elasticities through Monte Carlo (MC) simulations.
Conclusion: The parameter estimation within the linlog kinetic framework as presented here allows the determination of the elasticities directly from experimental data from typical dynamic and/or steady state experiments. These elasticities allow the reconstruction of the full kinetic model of Saccharomyces cerevisiae, and the determination of the control coefficients. MC simulations revealed that certain elasticities are potentially unidentifiable from dynamic data only. Addition of steady state perturbation of enzyme activities solved this problem.
Figures
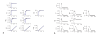

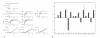
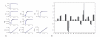
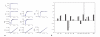
Similar articles
-
Determination of elasticities, concentration and flux control coefficients from transient metabolite data using linlog kinetics.Metab Eng. 2005 Mar;7(2):142-53. doi: 10.1016/j.ymben.2004.12.002. Metab Eng. 2005. PMID: 15781422
-
Model reduction and a priori kinetic parameter identifiability analysis using metabolome time series for metabolic reaction networks with linlog kinetics.Metab Eng. 2009 Jan;11(1):20-30. doi: 10.1016/j.ymben.2008.07.004. Epub 2008 Aug 5. Metab Eng. 2009. PMID: 18718548
-
Towards a genome-scale kinetic model of cellular metabolism.BMC Syst Biol. 2010 Jan 28;4:6. doi: 10.1186/1752-0509-4-6. BMC Syst Biol. 2010. PMID: 20109182 Free PMC article.
-
Approximative kinetic formats used in metabolic network modeling.Biotechnol Bioeng. 2005 Sep 5;91(5):534-45. doi: 10.1002/bit.20558. Biotechnol Bioeng. 2005. PMID: 16003779 Review.
-
Kinetic Modeling of Saccharomyces cerevisiae Central Carbon Metabolism: Achievements, Limitations, and Opportunities.Metabolites. 2022 Jan 13;12(1):74. doi: 10.3390/metabo12010074. Metabolites. 2022. PMID: 35050196 Free PMC article. Review.
Cited by
-
Dynamics and control of the central carbon metabolism in hepatoma cells.BMC Syst Biol. 2010 Apr 28;4:54. doi: 10.1186/1752-0509-4-54. BMC Syst Biol. 2010. PMID: 20426867 Free PMC article.
-
Structural control of metabolic flux.PLoS Comput Biol. 2013;9(12):e1003368. doi: 10.1371/journal.pcbi.1003368. Epub 2013 Dec 19. PLoS Comput Biol. 2013. PMID: 24367246 Free PMC article.
-
Microbiome distribution modeling using gradient descent strategies for mock, in vitro and clinical community distributions.PLoS One. 2023 Aug 21;18(8):e0290082. doi: 10.1371/journal.pone.0290082. eCollection 2023. PLoS One. 2023. PMID: 37603566 Free PMC article.
-
KiMoSys: a web-based repository of experimental data for KInetic MOdels of biological SYStems.BMC Syst Biol. 2014 Aug 13;8:85. doi: 10.1186/s12918-014-0085-3. BMC Syst Biol. 2014. PMID: 25115331 Free PMC article.
-
Systematic applications of metabolomics in metabolic engineering.Metabolites. 2012 Dec 14;2(4):1090-122. doi: 10.3390/metabo2041090. Metabolites. 2012. PMID: 24957776 Free PMC article.
References
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Molecular Biology Databases

