Resolution limit in community detection
- PMID: 17190818
- PMCID: PMC1765466
- DOI: 10.1073/pnas.0605965104
Resolution limit in community detection
Abstract
Detecting community structure is fundamental for uncovering the links between structure and function in complex networks and for practical applications in many disciplines such as biology and sociology. A popular method now widely used relies on the optimization of a quantity called modularity, which is a quality index for a partition of a network into communities. We find that modularity optimization may fail to identify modules smaller than a scale which depends on the total size of the network and on the degree of interconnectedness of the modules, even in cases where modules are unambiguously defined. This finding is confirmed through several examples, both in artificial and in real social, biological, and technological networks, where we show that modularity optimization indeed does not resolve a large number of modules. A check of the modules obtained through modularity optimization is thus necessary, and we provide here key elements for the assessment of the reliability of this community detection method.
Conflict of interest statement
The authors declare no conflict of interest.
Figures
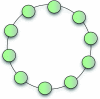
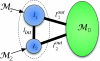
 1 and
1 and  2, the oval on the right represents the rest of the network
2, the oval on the right represents the rest of the network  0, whose structure is arbitrary.
0, whose structure is arbitrary.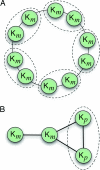
References
-
- Newman MEJ. Eur Phys J B. 2004;38:321–330.
-
- Danon L, Díaz-Guilera A, Duch J, Arenas A. J Stat Mech. 2005 P09008.
-
- Barabási A-L, Albert R. Rev Mod Phys. 2002;74:47–97.
-
- Dorogovtsev SN, Mendes JFF. Evolution of Networks: From Biological Nets to the Internet and WWW. Oxford: Oxford Univ Press; 2003.
-
- Newman MEJ. SIAM Rev. 2003;45:167–256.
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources

