Studying multisite binary and ternary protein interactions by global analysis of isothermal titration calorimetry data in SEDPHAT: application to adaptor protein complexes in cell signaling

Abstract

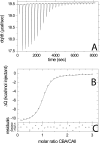
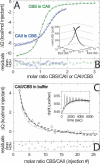
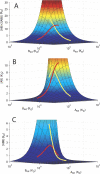
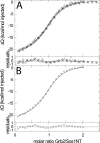
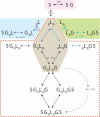
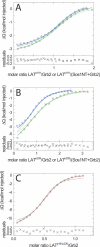
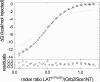
Multisite interactions and the formation of ternary or higher-order protein complexes are ubiquitous features of protein interactions. Cooperativity between different ligands is a hallmark for information transfer, and is frequently critical for the biological function. We describe a new computational platform for the global analysis of isothermal titration calorimetry (ITC) data for the study of binary and ternary multisite interactions, implemented as part of the public domain multimethod analysis software SEDPHAT. The global analysis of titrations performed in different orientations was explored, and the potential for unraveling cooperativity parameters in multisite interactions was assessed in theory and experiment. To demonstrate the practical potential and limitations of global analyses of ITC titrations for the study of cooperative multiprotein interactions, we have examined the interactions of three proteins that are critical for signal transduction after T-cell activation, LAT, Grb2, and Sos1. We have shown previously that multivalent interactions between these three molecules promote the assembly of large multiprotein complexes important for T-cell receptor activation. By global analysis of the heats of binding observed in sets of ITC injections in different orientations, which allowed us to follow the formation of binary and ternary complexes, we observed negative and positive cooperativity that may be important to control the pathway of assembly and disassembly of adaptor protein particles.

Figure 1.

ITC titration of a model 1:1 interaction: the binding of CBS to CAII. (A) Raw measured heat changes as a function of time, injecting 720 μM CBS into 35 μM CAII at 25°C. (B) Normalized measured heats of injection (circles), best-fit values (solid line). Parameter estimates were K = 1.22 × 10⁶/M and ΔH = −10.65 kcal/mol, f _CAII = 0.012, baseline = −0.143 kcal/mol. (C) Residuals of the fit with a RMSD of 0.050 kcal/mol.

Figure 2.

Global analysis of the binding of CBS to CAII by pairs of reverse titrations and a dissociation titration. (A) Injection of 720 μM CBS into 35 μM CAII (green squares) and 300 μM CAII into 30 μM CBS (blue circles). Colored solid lines are the global best-fit to both titrations, with best-fit parameter estimates of K = 1.46 × 10⁶/M and ΔH = −10.44 kcal/mol, with incompetent fractions of f _CAII = 0.01 for the titration of CBS into CAII and f _CAII = 0.21 for CAII into CBS. Bold black dotted lines (virtually superimposing the solid lines) are best-fit isotherms of a global fit, including additionally the dissociation titration. The inset depicts the cumulative experimental heats in both titrations. (B) Residuals of the fits. (C) Dissociation titration of 100 μM equimolar mixture of CAII and CBS into buffer (triangles), and best-fit isotherm (solid line). In this experiment, the syringe holds preformed CAII/CBS, which is injected into the cell containing initially only buffer. The dilution of the complex induces dissociation, causing uptake of heat. This configuration is similar to that used for the study of protein self-association (Arnaud and Bouteiller 2004; Luke et al. 2005). If these data are also included in the global fit with the data in A, global parameter estimates were K = 1.40 × 10⁶/M and ΔH = −10.50 kcal/mol, and local parameters for the dissociation experiment were f _CAII = 0.01 and a slope of −58 cal per injection (bold dotted line). The thin dotted line is the best-fit of the global analysis without allowing for a slope in the isotherm. The inset shows the raw data of the titration experiment. (D) Residuals to the dissociation data of the global fit including baseline slope.

Figure 3.

Theoretical binding isotherms for a molecule A with two equivalent sites for molecule B, and trajectories of orthogonal titration series. Depicted are the two-dimensional isotherm surfaces as a function of total A and total B. The concentrations of complex in the two-dimensional isotherm is visualized by the color temperature, and by the thin black lines following cross-sections of constant A_tot and B_tot, respectively. In this calculation, the macroscopic binding constant for occupation of the first site A + B ↔ AB is K _A = 1, with 10-fold negative cooperativity for occupation of the second site AB + B ↔ ABB. Titration experiments were simulated with a macromolecular concentration 15, a syringe concentration of 150, and 30 injections of 10 μL in an initial cell volume of 1414.1 μL. The red and yellow lines depict the binding along titrations of A into B and B into A, respectively, in analogy to the experimental data in the inset of Figure 2A. (A) Total concentration of bound B as a function of total concentrations of A and B. (B) Concentration of singly occupied A. (C) Concentration of fully occupied A.

Figure 4.

Relative error estimates for the parameters of the two-site interactions comparing single titration analysis relative to global titration analysis for a range of cooperativity constants α (with noncooperative sites at α = 0.25). Titration data were simulated along the trajectories described in Figure 3, with ΔH _AB = −10.0 kcal/mol and ΔH _ABB = 2ΔH _AB + ΔΔH _α, for parameter pairs {α,ΔΔH _α/(kcal/mol)} of {0.025, 1.25}, {0.0625, 0.75}, {0.125, 0.375}, {0.25, 0}, {0.5, −0.375}, {1, −0.75}, and {2.5, −1.125}. To each data set, 0.050 kcal/mol normally distributed noise was added. The error estimates σ for each parameter were determined from a model assuming unknown binding parameters, incompetent fractions, and a constant baseline offset, using Monte-Carlo error analysis. Ratios of errors are plotted for the titration of B into A (open symbols) and B into A (solid symbols), for the log₁₀ of the binding constant (squares), ΔH _AB (circles), α (up triangles), and ΔΔH _α (down triangles).

Figure 5.

Analysis of the interaction of Sos1NT and Grb2. (A) Titration of 75 μM Grb2 into 5.5 μM Sos1NT, with three replicates (symbols). (B) Titration of 75 μM Grb2 into 6 μM Sos1NT (circles) from a different preparation. The global analysis of the data shown in A and B was performed with incompetent Sos1NT (f _S) as a parameter local to each titration, and with all binding parameters as global parameters. This resulted in best-fit estimates of K _GS = (2.99 ± 0.13) × 10⁶/M and ΔH _GS = (−23.7 ± 0.3) kcal/mol (solid lines). Residuals to the data shown are at the bottom of each panel.

Figure 6.

Different possible complexes in the interaction of the two singly and the doubly phosphorylated LAT (_pL, L_p, and _pL_p), with Grb2 (G) and Sos1NT (S). The shaded areas and the red dotted line encompass reaction paths that can be studied separately. The numbers at the arrows for reactions forming binary complex are the determined free energies of binding in kcal/mol. In this model, it was assumed that phosphorylation of LAT on Y191 does not influence the thermodynamic parameters of Grb2 binding to pY226, and vice versa. For higher order complexes, the values indicated by Δ are the difference between the free energy of the complex and the sum of the free energy measured separately for each interface. The dotted arrow from G_pL_pG to SG_pL_pGS indicates that the additional free energy of binding cannot be assigned to addition of one or both Sos1NT.

Figure 7.

(A) Analysis of the ternary interaction of singly phosphorylated LAT^pY191 with Grb2 and Sos1NT, indicated as green-shaded area in Figure 6. Shown is a titration of 50 μM LAT^pY191 into 6.2 μM Grb2 (blue squares), and a titration of 50 μM LAT^pY191 into a mixture of 5.8 μM Grb2 and 5.8 μM Sos1NT (green crosses) at a temperature of 25°C. In the global analysis, three more replicate titrations are included (data not shown), incompetent LAT^pY191 is considered as a global parameter for all titrations, and incompetent Grb2 is considered as a local parameter only for the LAT^pY191 into Grb2 titrations. The parameter values for the Grb2-Sos1NT interaction are fixed to those derived from the analysis shown in Figure 5, and treated as prior knowledge. The best-fit isotherms (solid lines) are obtained for parameter estimates of K _LpG = 3.5 × 10⁶/M, ΔH _LpG = −3.9 kcal/mol, with cooperativity ΔΔG _LpGS = 0.37 kcal/mol and ΔΔH _LpGS = −3.9 kcal/mol. For comparison, the best-fit assuming the absence of cooperativity is shown as dotted lines, which give a 2.6-fold increase in the global χ² of the fit. (B) Equivalent ternary interaction analysis of Grb2 and Sos1NT with LAT^pY226, singly phosphorylated at Y226 (blue-shaded area in Fig. 6). Shown is a titration of 100 μM LAT^pY226 into 4.5 μM Grb2 (blue squares), and a titration of 50 μM LAT^pY226 into a mixture of 3.5 μM Grb2 and 3.5 μM Sos1NT (green crosses) at a temperature of 25°C. The analysis of these data analogous to that in A, jointly with one additional experiment for each orientation, results in global best-fit estimates of K _GpL = 1.7 × 10⁶/M, ΔH _GpL = −6.8 kcal/mol, with cooperativity ΔΔG _SGpL = 0.61 kcal/mol and ΔΔH _SGpL = −12.7 kcal/mol (solid lines). For comparison, again, the best-fit assuming the absence of cooperativity is shown as dotted lines, respectively, which gives a 2.7-fold increase in the global χ² of the fit. (C) Analysis of the multisite binary interaction of doubly phosphorylated LAT with Grb2. Shown are data from the injection of 40 μM LAT^pY191pY226 into 4.5 μM Grb2 (crosses). Here, the microscopic binding constants to the sites pY191 and pY226 were taken from the analysis with singly phosphorylated LAT peptide as shown in A and B. Both fractions of incompetent LAT^pY191pY226 and Grb2 were considered. The dotted line indicates the best-fit assuming the absence of cooperativity between these sites. The solid line is the best-fit model including cooperativity, with ΔΔG _GpLpG = 0.33 kcal/mol and ΔΔH _GpLpG = −3.2 kcal/mol.

Figure 8.

Ternary interaction of doubly phosphorylated LAT^pY191pY226 with Grb2 and Sos1NT. Two titrations are shown of 40 μM LAT^pY191pY226 into equimolar mixtures of 4 μM Grb2 and 4 μM Sos1NT. In the joint analysis, only LAT^pY191pY226 was considered to contain incompetent fractions. The dotted line is the best-fit isotherm including all predetermined binding and cooperativity parameters for the binary and ternary complex formation (for complexes GL, LG GLG, LGS, SGL) as shown in Figures 5 and 7, and assuming that the formation of quadruple and quintuple complexes (SGLG, GLGS, SGLGS) can be predicted from the parameters obtained for the formation of the triple complexes SGL, LGS, and GLG, respectively, without invoking additional cooperativity. The solid line is the best-fit isotherm permitting cooperativity in that the addition of Sos1NT to preformed GLGS (or SGLG, respectively) is different from the addition of Sos1NT to preformed GL (or LG, respectively). For example, such cooperativity could be theoretically imagined to arise from Sos1NT-Sos1NT contacts in the quintuple complex. With this model, the solid lines show the calculated best-fit isotherm for additional stabilizing free energy of binding for the quintuple complex of ΔΔG _SGpLpGS = −0.97 kcal/mol and ΔΔH _SGpLpGS = 6.5 kcal/mol.