Theory of lethal mutagenesis for viruses
- PMID: 17202214
- PMCID: PMC1865999
- DOI: 10.1128/JVI.01624-06
Theory of lethal mutagenesis for viruses
Abstract
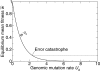
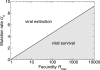
Mutation is the basis of adaptation. Yet, most mutations are detrimental, and elevating mutation rates will impair a population's fitness in the short term. The latter realization has led to the concept of lethal mutagenesis for curing viral infections, and work with drugs such as ribavirin has supported this perspective. As yet, there is no formal theory of lethal mutagenesis, although reference is commonly made to Eigen's error catastrophe theory. Here, we propose a theory of lethal mutagenesis. With an obvious parallel to the epidemiological threshold for eradication of a disease, a sufficient condition for lethal mutagenesis is that each viral genotype produces, on average, less than one progeny virus that goes on to infect a new cell. The extinction threshold involves an evolutionary component based on the mutation rate, but it also includes an ecological component, so the threshold cannot be calculated from the mutation rate alone. The genetic evolution of a large population undergoing mutagenesis is independent of whether the population is declining or stable, so there is no runaway accumulation of mutations or genetic signature for lethal mutagenesis that distinguishes it from a level of mutagenesis under which the population is maintained. To detect lethal mutagenesis, accurate measurements of the genome-wide mutation rate and the number of progeny per infected cell that go on to infect new cells are needed. We discuss three methods for estimating the former. Estimating the latter is more challenging, but broad limits to this estimate may be feasible.
Figures


References
-
- Anderson, J. P., R. Daifuku, and L. A. Loeb. 2004. Viral error catastrophe by mutagenic nucleosides. Annu. Rev. Microbiol. 58:183-205. - PubMed
-
- Anderson, R. M., and R. M. May. 1991. Infectious diseases of humans: dynamics and control. Oxford University Press, Oxford, United Kingdom.
-
- Bateman, A. J. 1959. The viability of near-normal irradiated chromosomes. Int. J. Radiat. Biol. 1:170-180.
-
- Bell, G. 1982. The masterpiece of nature: the evolution and genetics of sexuality. University of California Press, Berkeley, CA.
-
- Bordería, A. V., F. M. Codoñer, and R. Sanjuán. Selection drives organ compartmentalization in HIV-1: evidence from gag and pol genes. Evolution, in press. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Research Materials

