One, two, three, four, nothing more: an investigation of the conceptual sources of the verbal counting principles

Abstract

Since the publication of [Gelman, R., & Gallistel, C. R. (1978). The child's understanding of number. Cambridge, MA: Harvard University Press.] seminal work on the development of verbal counting as a representation of number, the nature of the ontogenetic sources of the verbal counting principles has been intensely debated. The present experiments explore proposals according to which the verbal counting principles are acquired by mapping numerals in the count list onto systems of numerical representation for which there is evidence in infancy, namely, analog magnitudes, parallel individuation, and set-based quantification. By asking 3- and 4-year-olds to estimate the number of elements in sets without counting, we investigate whether the numerals that are assigned cardinal meaning as part of the acquisition process display the signatures of what we call "enriched parallel individuation" (which combines properties of parallel individuation and of set-based quantification) or analog magnitudes. Two experiments demonstrate that while "one" to "four" are mapped onto core representations of small sets prior to the acquisition of the counting principles, numerals beyond "four" are only mapped onto analog magnitudes about six months after the acquisition of the counting principles. Moreover, we show that children's numerical estimates of sets from 1 to 4 elements fail to show the signature of numeral use based on analog magnitudes - namely, scalar variability. We conclude that, while representations of small sets provided by parallel individuation, enriched by the resources of set-based quantification are recruited in the acquisition process to provide the first numerical meanings for "one" to "four", analog magnitudes play no role in this process.

Figure 1

Average numeral by set size functions for subset-knowers. “One”- and “two”-knowers were combined because their functions were not significantly different from each other; as were “three”- and “four”-knowers.

Figure 2

Distribution of the slopes of the linear fits of CP-knowers' average numeral by set size functions for set sizes between 6 and 10. Each bar represents the number of CP-knowers with 6–10 slopes of a given size.

Figure 3

Average numeral by set size functions for CP non-mappers (solid line) and CP mappers (dashed line). CP non-mappers were CP-knowers who had functions with slopes that were less than 0.3 in the unambiguous magnitude range (6–10); CP mappers had 6–10 slopes that were greater than 0.3.

Figure 4

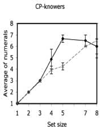
Numeral distributions for CP non-mappers and CP mappers. Each distribution represents the probability of using a given numeral as a function of set size. For example, for sets of 1 object, the distribution for “one” shows how often children applied “one” to this set size out of all trials with this set size. Figures in the left column show the distributions for “one” to “four” (“one”: ; “two”: ; “three”: ; “four”: ). Figures in the right column show the distributions for “five” (), “six” (), “seven” and “eight” (); “nine” and “ten” (); and all numerals beyond “ten” (). The distributions for “seven” and “eight” were added together to simplify the figures as were the distributions for “nine” and “ten” and the distributions for numerals greater than “ten”.

Figure 5

Accuracy (in percent correct) of children’s non-verbal judgments as a function of comparison type (2 vs. 3, 2 vs. 6, 6 vs. 10, 8 vs. 10) and knower-level.

Figure 6

Average numeral by set size functions for subset-knowers tested on What’s on this Card?. “Four”-knowers were grouped with “three”-knowers because there were only three of them.

Figure 7

Average numeral by set size functions for CP non-mappers (continuous line) and for CP mappers (dashed line). CP non-mappers were CP-knowers who had functions with 5–8 slopes that were less than 0.3; CP mappers had 5–8 slopes that were greater than 0.3.