Mesoscale simulation of blood flow in small vessels

Abstract

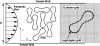
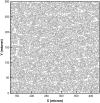
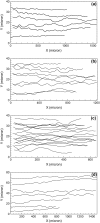
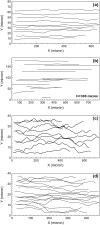
Computational modeling of blood flow in microvessels with internal diameter 20-500 microm is a major challenge. It is because blood in such vessels behaves as a multiphase suspension of deformable particles. A continuum model of blood is not adequate if the motion of individual red blood cells in the suspension is of interest. At the same time, multiple cells, often a few thousands in number, must also be considered to account for cell-cell hydrodynamic interaction. Moreover, the red blood cells (RBCs) are highly deformable. Deformation of the cells must also be considered in the model, as it is a major determinant of many physiologically significant phenomena, such as formation of a cell-free layer, and the Fahraeus-Lindqvist effect. In this article, we present two-dimensional computational simulation of blood flow in vessels of size 20-300 microm at discharge hematocrit of 10-60%, taking into consideration the particulate nature of blood and cell deformation. The numerical model is based on the immersed boundary method, and the red blood cells are modeled as liquid capsules. A large RBC population comprising of as many as 2500 cells are simulated. Migration of the cells normal to the wall of the vessel and the formation of the cell-free layer are studied. Results on the trajectory and velocity traces of the RBCs, and their fluctuations are presented. Also presented are the results on the plug-flow velocity profile of blood, the apparent viscosity, and the Fahraeus-Lindqvist effect. The numerical results also allow us to investigate the variation of apparent blood viscosity along the cross-section of a vessel. The computational results are compared with the experimental results. To the best of our knowledge, this article presents the first simulation to simultaneously consider a large ensemble of red blood cells and the cell deformation.

FIGURE 1

Schematic of the computational domain, and the Eulerian and Lagrangian grids.

FIGURE 2

Motion of an isolated RBC in parabolic flow through a 40-μm channel. The flow is from left to right and the center of the channel is shown by (- · - · - · -). (a) Normal, deformable RBC; (b) less deformable RBC; and (c) RBC with reduced membrane resistance. A point on the cell surface is shown to illustrate the tank-treading motion.

FIGURE 3

(a) The x-y trajectory, (b) longitudinal velocity, and (c) lateral velocity of the cells shown in Fig. 2. (··· ···) Normal cell (case a in Fig. 2); (——) less deformable cell (case b); (- - - -) cells with reduced membrane resistance (case c).

FIGURE 4

RBC suspension in a 20-μm channel. (a) Normal RBC at H_t = 20% (H_d = 30%); (b) normal RBC at H_t = 48% (H_d = 60%); and (c) less deformable RBCs at H_t = 20% (H_d = 30%). For each case, three time instances are shown. The mean velocities are (a) 7.5 mm/s; (b) 3.5 mm/s; and (c) 4.7 mm/s. The third plots for panels a–c represent ∼500 ms after the onset of flow.

FIGURE 5

Suspension of normal RBCs at H_d = 45% in (a) 80-μm channel, and in (b) 150-μm channel. The tube hematocrits are 38% and 43%, respectively. The computation domain contains 160 cells in panel a and 600 cells in panel b. Mean velocities are (a) 5 mm/s, (b) 6.5 mm/s. The figures represent ∼300 ms after the onset of flow.

FIGURE 6

Suspension of normal RBCs in 300-μm channel at H_d = 45% (H_t = 44%). A total of 2500 cells are simulated in the computation domain as shown above. Mean velocity is 12 mm/s. The figure represents ∼150 ms after the onset of flow.

FIGURE 7

Suspension of less deformable RBCs at H_d = 45% in (a) 80-μm channel and (b) 150-μm channel. The tube hematocrits are 38% and 43%, respectively. The computation domain contains 160 cells in panel a and 600 cells in panel b. Mean velocities are (a) 3.6 mm/s and (b) 4.9 mm/s. The figures represent 300 ms after the onset of flow.

FIGURE 8

Trajectory of normal red blood cells in suspension flowing through a vessel. Panels a–c represent a 40-μm channel at H_d = 10, 20, and 60%, respectively. Corresponding tube hematocrits are 6.4, 13.5, and 50%. (d) 150-μm channel at H_d = 20% (H_t = 18%). For panel d, only half of the channel is shown.

FIGURE 9

Trajectory of red blood cells in suspension flowing through a vessel. (a) Normal cells in a 150-μm channel at H_d = 45% (H_t = 43%); (b) normal cells in a 300-μm channel H_d = 45% (H_t = 44%); (c) less deformable cells in a 40-μm channel at H_d = 20% (H_t = 13.5%); and (d) fewer deformable cells in a 40-μm channel at H_d = 60% (H_t = 50%). In panels a and b, only half of the channel is shown.

FIGURE 10

Velocity traces of red blood cells in suspension flowing through a 40-μm channel. (a) Normal cells at H_d = 20% (H_t = 13.5%); (b) normal cells at H_d = 60% (H_t = 50%); and (c) less deformable cells at H_d = 20% (H_t = 13.5%). Mean velocity of whole blood for various cases can be found from Table 2. The velocity of RBCs is scaled with the centerline velocity.

FIGURE 11

RMS fluctuations in lateral position of red blood cells in suspension. Symbols are present numerical simulations. Range of data obtained from the experiments (2) is also shown.

FIGURE 12

Coefficient of variation of red blood cell velocity in a 40-μm channel. Symbols are the present numerical simulations. Thick lines are the best fit through the numerical data. Thin line is the best fit from experimental results (2).

FIGURE 13

Average velocity profile of blood. Dotted line is the parabolic flow. Thick lines represent suspension of normal, deformable RBCs, and thin lines represent suspension of less deformable RBCs. (– – – –) H_d = 20%; ( – · – · –) H_d = 45%; and (– · · – · · –) H_d = 60%. In plot d, the solid line represents the 300-μm channel at H_d = 45%. The corresponding tube hematocrit can be found from Table 1. Mean velocities are listed in Table 2.

FIGURE 14

Dimensionless cell-free layer δ/(H/2). Lines are analytical modeling (13), and open symbols are in vitro data (4). Solid symbols are the results from the present numerical simulation.

FIGURE 15

The Fahraeus-Lindqvist effect: the relative viscosity of blood as a function of vessel size and discharge hematocrit. The three solid lines represent the empirical expression given in Pries et al. (3) based on in vitro data. The symbols are the data from the present numerical simulation. The tube hematocrit values for a channel size are given in Table 1.

FIGURE 16

The variation of local effective viscosity along the wall-normal direction across the channel. Here y/(H/2) = 0 is the center of the channel, and y/(H/2) = 1 is the wall. The asterisk denotes less deformable cells. All other cases are for normal cells.