Part 1. Automated change detection and characterization in serial MR studies of brain-tumor patients
- PMID: 17216385
- PMCID: PMC3043896
- DOI: 10.1007/s10278-006-1038-1
Part 1. Automated change detection and characterization in serial MR studies of brain-tumor patients
Abstract
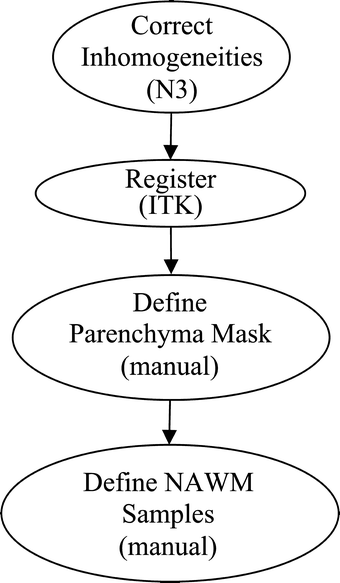
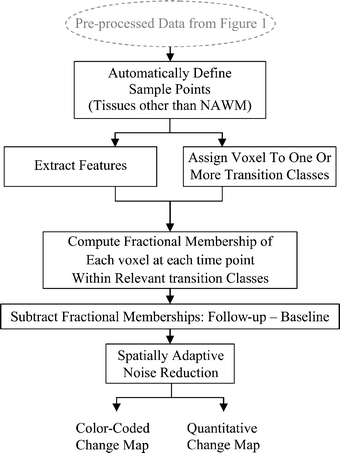
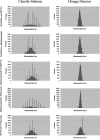
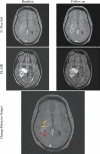
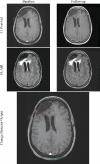
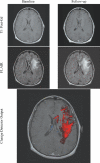
The goal of this study was to create an algorithm which would quantitatively compare serial magnetic resonance imaging studies of brain-tumor patients. A novel algorithm and a standard classify-subtract algorithm were constructed. The ability of both algorithms to detect and characterize changes was compared using a series of digital phantoms. The novel algorithm achieved a mean sensitivity of 0.87 (compared with 0.59 for classify-subtract) and a mean specificity of 0.98 (compared with 0.92 for classify-subtract) with regard to identification of voxels as changing or unchanging and classification of voxels into types of change. The novel algorithm achieved perfect specificity in seven of the nine experiments. The novel algorithm was additionally applied to a short series of clinical cases, where it was shown to identify visually subtle changes. Automated change detection and characterization could facilitate objective review and understanding of serial magnetic resonance imaging studies in brain-tumor patients.
Figures

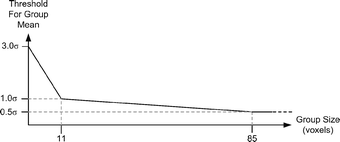
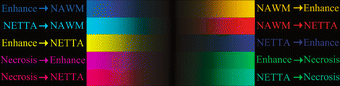
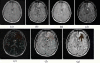

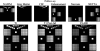


References
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Medical

