A proposal for robust temperature compensation of circadian rhythms

Abstract

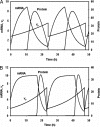
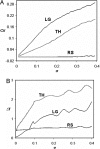
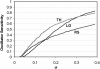
The internal circadian rhythms of cells and organisms coordinate their physiological properties to the prevailing 24-h cycle of light and dark on earth. The mechanisms generating circadian rhythms have four defining characteristics: they oscillate endogenously with period close to 24 h, entrain to external signals, suffer phase shifts by aberrant pulses of light or temperature, and compensate for changes in temperature over a range of 10 degrees C or more. Most theoretical descriptions of circadian rhythms propose that the underlying mechanism generates a stable limit cycle oscillation (in constant darkness or dim light), because limit cycles quite naturally possess the first three defining properties of circadian rhythms. On the other hand, the period of a limit cycle oscillator is typically very sensitive to kinetic rate constants, which increase markedly with temperature. Temperature compensation is therefore not a general property of limit cycle oscillations but must be imposed by some delicate balance of temperature dependent effects. However, "delicate balances" are unlikely to be robust to mutations. On the other hand, if circadian rhythms arise from a mechanism that concentrates sensitivity into a few rate constants, then the "balancing act" is likely to be more robust and evolvable. We propose a switch-like mechanism for circadian rhythms that concentrates period sensitivity in just two parameters, by forcing the system to alternate between a stable steady state and a stable limit cycle.

Fig. 1.

One-parameter bifurcation diagrams for the differential equations (B1) and (B2), described in Appendix. (A) Parameter values: v_m = 2, k_m = 0.2, k_p1 = 53.36, k_p2 = 0.06, k_p3 = 0.2, K_eq = 1, P_crit = 0.6, J_p = 0.05. (B) All rate constants increased 2-fold. For each value of the bifurcation parameter, v_p, we plot the value of [PER] on recurrent solutions of the differential equations (steady states and limit cycle oscillations). Solid curve, stable steady state; dashed curve, unstable steady state. Curves labeled [PER]_max and [PER]_min indicate the range of an oscillatory solution at fixed value of v_p. At the Hopf bifurcation, the steady state changes stability and small amplitude, stable limit cycle oscillations arise. At the SNIC bifurcation, two steady states (a stable node and an unstable saddle) annihilate each other and are replaced by a large amplitude limit cycle. (A Inset) The period of oscillation at the SNIC bifurcation is infinite, but drops quickly to a value of ≈15 h. Superimposed on the bifurcation diagrams are the trajectories (dashed/dotted line) generated by the resetting hypothesis (see text). Although the locations of the bifurcation points depend strongly on parameter values, as do the shapes of the resetting trajectories (dashed/dotted line), the period of the two trajectories is precisely 24 h.

Fig. 2.

Time courses of per mRNA and protein, and the resetting parameter, v_p, for the mechanism described in the text. (A) Parameter values as in Fig. 1A, plus P_thresh = 2, μ = 0.0288, σ = 0.5. (B) Parameter values as in Fig. 1B, plus P_thresh = 2, μ = 0.0576, σ = 0.25.

Fig. 3.

Robustness of compensated oscillator period as a function of perturbation strength (σ_p) for the models LG, TH and RS. (A) The CV of the period is plotted vs. σ_p, indicating each model's response to test A. RS is virtually unaffected (extremely robust), whereas LG and TH fail to compensate the period to different degrees. (B) ΔT is averaged over all possible single reaction mutants (Test B) for a given perturbation strength, σ_p. We see that RS is robustly temperature compensated for such mutations (very low ΔT), whereas both LG and TH fail to compensate over the given temperature range.

Fig. 4.

Sensitivity of oscillation (% of samples that lose oscillation) as a function of perturbation strength (σ_p) in test A. At σ_p = 0.2, LG loses oscillation ≈47% of the time, TH ≈59% of the time, and RS ≈40% of the time. Oscillations are most robust to small perturbations for LG, whereas RS is considerably more robust than either LG or TH for large perturbations.