Inference of population structure under a Dirichlet process model

Abstract

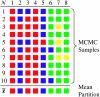
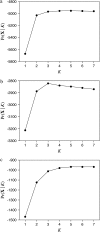
Inferring population structure from genetic data sampled from some number of individuals is a formidable statistical problem. One widely used approach considers the number of populations to be fixed and calculates the posterior probability of assigning individuals to each population. More recently, the assignment of individuals to populations and the number of populations have both been considered random variables that follow a Dirichlet process prior. We examined the statistical behavior of assignment of individuals to populations under a Dirichlet process prior. First, we examined a best-case scenario, in which all of the assumptions of the Dirichlet process prior were satisfied, by generating data under a Dirichlet process prior. Second, we examined the performance of the method when the genetic data were generated under a population genetics model with symmetric migration between populations. We examined the accuracy of population assignment using a distance on partitions. The method can be quite accurate with a moderate number of loci. As expected, inferences on the number of populations are more accurate when theta = 4N(e)u is large and when the migration rate (4N(e)m) is low. We also examined the sensitivity of inferences of population structure to choice of the parameter of the Dirichlet process model. Although inferences could be sensitive to the choice of the prior on the number of populations, this sensitivity occurred when the number of loci sampled was small; inferences are more robust to the prior on the number of populations when the number of sampled loci is large. Finally, we discuss several methods for summarizing the results of a Bayesian Markov chain Monte Carlo (MCMC) analysis of population structure. We develop the notion of the mean population partition, which is the partition of individuals to populations that minimizes the squared partition distance to the partitions sampled by the MCMC algorithm.

Figure 1.—

Example of the calculation of the mean partition. The mean partition, , minimizes the sum of the squared distances to the partitions sampled by the MCMC algorithm.

Figure 2.—

The mean partitions for analyses of the Imapala Aegyceros melampus data (Lorenzen et al. 2004, 2006). Analyses were performed in which the number of populations was fixed (K = 1, K = 2, K = 3, K = 4, K = 5, K = 6, K = 7) or in which the number of populations was a random variable with a Dirichlet process prior [E(K) = 2, E(K) = 5, E(K) = 10, E(K) = 20]. The assignment of individuals (boxes) is indicated by color.

Figure 3.—

The mean partitions for analyses of the Taita thrush data (Galbusera et al. 2000). Analyses were performed in which the number of populations was fixed (K = 1, K = 2, K = 3, K = 4, K = 5, K = 6, K = 7) or in which the number of populations was a random variable with a Dirichlet process prior [E(K) = 2, E(K) = 5, E(K) = 10, E(K) = 20]. The assignment of individuals (boxes) is indicated by color.

Figure 4.—

The mean partitions for analyses of the Mus musculus data (Orth et al. 1998). Analyses were performed in which the number of populations was fixed (K = 1, K = 2, K = 3, K = 4, K = 5, K = 6, K = 7) or in which the number of populations was a random variable with a Dirichlet process prior [E(K) = 2, E(K) = 5, E(K) = 10, E(K) = 20]. The assignment of individuals (boxes) is indicated by color.

Figure 5.—

The probabilities and Bayes' factors of all pairs of individuals being grouped together into the same population. Each triangle shows all pairs of individuals. The top left corner of a triangle shows the probability/Bayes' factor for individuals 1 and 2, the top right corner of the triangle shows the probability/Bayes' factor for individuals 1 and n, and the bottom corner of the triangle shows the probability/Bayes' factor for individuals n − 1 and n. Generally speaking, Bayes' factors >10 are strong evidence for two individuals being grouped together in the same population whereas Bayes' factors are strong evidence against grouping two individuals into the same population. All analyses were run assuming a Dirichlet process prior on the number of populations and a prior mean for the number of populations of E(K) = 5.

Figure 6.—

The marginal likelihoods Pr(X | K) when the number of populations (K) is fixed to different values (K = 1, 2, …, 7). (a) Impala data (Lorenzen et al. 2004, 2006); (b) Taita thrush data (Galbusera et al. 2000); (c) Mus musculus data (Orth et al. 1998).

Figure 7.—

The prior, Pr(K), and posterior, Pr(K | X), probability distributions for the number of populations for the Impala data set when the prior mean of the number of populations varies.