Computational aspects of feedback in neural circuits
- PMID: 17238280
- PMCID: PMC1779299
- DOI: 10.1371/journal.pcbi.0020165
Computational aspects of feedback in neural circuits
Abstract
It has previously been shown that generic cortical microcircuit models can perform complex real-time computations on continuous input streams, provided that these computations can be carried out with a rapidly fading memory. We investigate the computational capability of such circuits in the more realistic case where not only readout neurons, but in addition a few neurons within the circuit, have been trained for specific tasks. This is essentially equivalent to the case where the output of trained readout neurons is fed back into the circuit. We show that this new model overcomes the limitation of a rapidly fading memory. In fact, we prove that in the idealized case without noise it can carry out any conceivable digital or analog computation on time-varying inputs. But even with noise, the resulting computational model can perform a large class of biologically relevant real-time computations that require a nonfading memory. We demonstrate these computational implications of feedback both theoretically, and through computer simulations of detailed cortical microcircuit models that are subject to noise and have complex inherent dynamics. We show that the application of simple learning procedures (such as linear regression or perceptron learning) to a few neurons enables such circuits to represent time over behaviorally relevant long time spans, to integrate evidence from incoming spike trains over longer periods of time, and to process new information contained in such spike trains in diverse ways according to the current internal state of the circuit. In particular we show that such generic cortical microcircuits with feedback provide a new model for working memory that is consistent with a large set of biological constraints. Although this article examines primarily the computational role of feedback in circuits of neurons, the mathematical principles on which its analysis is based apply to a variety of dynamical systems. Hence they may also throw new light on the computational role of feedback in other complex biological dynamical systems, such as, for example, genetic regulatory networks.
Conflict of interest statement
Figures



 over the difference of both input rates. Feedback values were injected as input currents into a randomly chosen subset of neurons in the circuit. Scale in nA shows average strength of feedback currents, also in (H). (E) Performance of linear readout that was trained to output 0 as long as CA(t) stayed below 0.83 nA, and to output r
2(t) once CA(t) had crossed this threshold, as long as CA(t) stayed above 0.66 nA (i.e., in this test run during the shaded time periods). (F) Performance of linear readout trained to output r
1(t) − CA(t), i.e., a combination of external and internal variables, at any time t (both r
1 and CA normalized into the range [0,1]). (G) Response of a randomly chosen neuron in the circuit for ten repetitions of the same experiment (with input spike trains generated by Poisson processes with the same time course of firing rates), showing biologically realistic trial-to-trial variability. (H) Activity traces of a continuous attractor as in (D), but in eight different trials for eight different fixed values of r
1 and r
2 (shown on the right).
over the difference of both input rates. Feedback values were injected as input currents into a randomly chosen subset of neurons in the circuit. Scale in nA shows average strength of feedback currents, also in (H). (E) Performance of linear readout that was trained to output 0 as long as CA(t) stayed below 0.83 nA, and to output r
2(t) once CA(t) had crossed this threshold, as long as CA(t) stayed above 0.66 nA (i.e., in this test run during the shaded time periods). (F) Performance of linear readout trained to output r
1(t) − CA(t), i.e., a combination of external and internal variables, at any time t (both r
1 and CA normalized into the range [0,1]). (G) Response of a randomly chosen neuron in the circuit for ten repetitions of the same experiment (with input spike trains generated by Poisson processes with the same time course of firing rates), showing biologically realistic trial-to-trial variability. (H) Activity traces of a continuous attractor as in (D), but in eight different trials for eight different fixed values of r
1 and r
2 (shown on the right).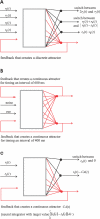

 1, …,
1, …,  k and suitable fading-memory readouts Ĥ
1, …, Ĥl (which may also be subject to noise). (B) Resulting noise-robust emulation of an arbitrary given FSM by adding feedback to the system in (A). The same readouts as in (A) (denoted CL − Ĥj(t) in the closed loop) now encode the current state of the simulated FSM.
k and suitable fading-memory readouts Ĥ
1, …, Ĥl (which may also be subject to noise). (B) Resulting noise-robust emulation of an arbitrary given FSM by adding feedback to the system in (A). The same readouts as in (A) (denoted CL − Ĥj(t) in the closed loop) now encode the current state of the simulated FSM.
Similar articles
-
Fading memory and kernel properties of generic cortical microcircuit models.J Physiol Paris. 2004 Jul-Nov;98(4-6):315-30. doi: 10.1016/j.jphysparis.2005.09.020. Epub 2005 Nov 28. J Physiol Paris. 2004. PMID: 16310350
-
Real-time computing without stable states: a new framework for neural computation based on perturbations.Neural Comput. 2002 Nov;14(11):2531-60. doi: 10.1162/089976602760407955. Neural Comput. 2002. PMID: 12433288
-
Spike frequency adaptation supports network computations on temporally dispersed information.Elife. 2021 Jul 26;10:e65459. doi: 10.7554/eLife.65459. Elife. 2021. PMID: 34310281 Free PMC article.
-
Input prediction and autonomous movement analysis in recurrent circuits of spiking neurons.Rev Neurosci. 2003;14(1-2):5-19. doi: 10.1515/revneuro.2003.14.1-2.5. Rev Neurosci. 2003. PMID: 12929914 Review.
-
Computational and in vitro studies of persistent activity: edging towards cellular and synaptic mechanisms of working memory.Neuroscience. 2006 Apr 28;139(1):135-51. doi: 10.1016/j.neuroscience.2005.06.011. Epub 2005 Dec 6. Neuroscience. 2006. PMID: 16337341 Review.
Cited by
-
Firing rate homeostasis counteracts changes in stability of recurrent neural networks caused by synapse loss in Alzheimer's disease.PLoS Comput Biol. 2020 Aug 25;16(8):e1007790. doi: 10.1371/journal.pcbi.1007790. eCollection 2020 Aug. PLoS Comput Biol. 2020. PMID: 32841234 Free PMC article.
-
Embedding multiple trajectories in simulated recurrent neural networks in a self-organizing manner.J Neurosci. 2009 Oct 21;29(42):13172-81. doi: 10.1523/JNEUROSCI.2358-09.2009. J Neurosci. 2009. PMID: 19846705 Free PMC article.
-
Domain-driven models yield better predictions at lower cost than reservoir computers in Lorenz systems.Philos Trans A Math Phys Eng Sci. 2021 Apr 5;379(2194):20200246. doi: 10.1098/rsta.2020.0246. Epub 2021 Feb 15. Philos Trans A Math Phys Eng Sci. 2021. PMID: 33583272 Free PMC article.
-
Heteroclinic networks for brain dynamics.Front Netw Physiol. 2023 Nov 8;3:1276401. doi: 10.3389/fnetp.2023.1276401. eCollection 2023. Front Netw Physiol. 2023. PMID: 38020242 Free PMC article. Review.
-
Reservoir Computing Properties of Neural Dynamics in Prefrontal Cortex.PLoS Comput Biol. 2016 Jun 10;12(6):e1004967. doi: 10.1371/journal.pcbi.1004967. eCollection 2016 Jun. PLoS Comput Biol. 2016. PMID: 27286251 Free PMC article.
References
-
- Douglas RJ, Koch C, Mahowald M, Martin K, Suarez H. Recurrent excitation in neocortical circuits. Science. 1995;269:981–985. - PubMed
-
- Grossberg S. How does the cerebral cortex work? Development, learning, attention, and 3D vision by laminar circuits of visual cortex. Behav Cogn Neurosci Rev. 2003;2:47–76. - PubMed
-
- Buonomano DV, Merzenich MM. Temporal information transformed into a spatial code by a neural network with realistic properties. Science. 1995;267:1028–1030. - PubMed
-
- Maass W, Sontag ED. Neural systems as nonlinear filters. Neural Computation. 2000;12:1743–1772. - PubMed
-
- Maass W, Natschläger T, Markram H. Real-time computing without stable states: A new framework for neural computation based on perturbations. Neural Computation. 2002;14:2531–2560. - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources
Molecular Biology Databases

