Stochastic amplification in epidemics

Abstract

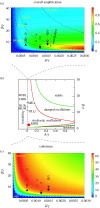
The role of stochasticity and its interplay with nonlinearity are central current issues in studies of the complex population patterns observed in nature, including the pronounced oscillations of wildlife and infectious diseases. The dynamics of childhood diseases have provided influential case studies to develop and test mathematical models with practical application to epidemiology, but are also of general relevance to the central question of whether simple nonlinear systems can explain and predict the complex temporal and spatial patterns observed in nature outside laboratory conditions. Here, we present a stochastic theory for the major dynamical transitions in epidemics from regular to irregular cycles, which relies on the discrete nature of disease transmission and low spatial coupling. The full spectrum of stochastic fluctuations is derived analytically to show how the amplification of noise varies across these transitions. The changes in noise amplification and coherence appear robust to seasonal forcing, questioning the role of seasonality and its interplay with deterministic components of epidemiological models. Childhood diseases are shown to fall into regions of parameter space of high noise amplification. This type of "endogenous" stochastic resonance may be relevant to population oscillations in nonlinear ecological systems in general.

Figure 1

(a) The open SIR model with immigration. We assume that susceptible individuals may acquire the infection not only as a result of internal transmission within their city, but also as a result of infection from an external source due to transient individual movements between cities. This formulation is the simplest way to take into account that real communities are not isolated, but spatially extended systems interconnected by migration (Rohani et al. 1999; Keeling et al. 2001; Lloyd & Jansen, 2002; Xia et al. 2004). (b) The graph shows a typical stochastic realization of the SIR model. The parameters used in the simulations are N=1.0×10⁵, η=1.0×10⁻⁵ d⁻¹, δ=5.5×10⁻⁵ d⁻¹ and the mean transmission rate β₀=1.175 d⁻¹. Disease parameters correspond to typical measles values from Keeling et al. (2001) and Bauch & Earn (2003b). The recovery rate γ was estimated here by aggregating the exposed and the infectious phases from SEIR models with an additional exposed class. No seasonal forcing is included (β₁=0). The model is simulated with the event algorithm of Gillespie (1976). Three different events are considered. Birth and death. Individuals in either class (S, I, R) die at a rate δ. Empty sites (E) are instantaneously replenished by births of new susceptibles at a rate b, where b=δ: $E\stackrel{\delta }{⟶}S$. Infection. Susceptible individuals acquire the infection at a rate η+βI/N, the total force of infection: $S\stackrel{\eta +\beta I/N}{⟶}I$. Recovery. Infectious individuals recover at a rate γ: $I\stackrel{\gamma }{⟶}R$.

Figure 2

Changes in the PSD as a function of a decreasing transmission rate. The analytical PSD (a) without seasonal forcing and the corresponding numerical PSD (b) without and (c) with school-term seasonal forcing are shown. In (b), the corresponding effective transmission rates 〈B〉 have been calculated (Keeling et al. 2001) for a more accurate comparison with (c) the seasonally forced case. (a) The analytical formula is given by equation (10) of the electronic supplementary material (see §2) to calculate the PSD for increasing values of the proportion of vaccination, p. As p increases, the effective transmission rate β decreases accordingly (see figure S2 of the electronic supplementary material and §2). A lower transmission rate changes the PSD by decreasing the overall amplitude of the oscillations, shifting the peak to lower frequencies and flattening the curve, so that cycles become less coherent as a broader range of frequencies contribute more equally to the fluctuations. This effect is seen in the numerical averaged PSD, regardless of the presence or absence of school-term seasonal forcing. When seasonality is considered, an annual strong peak arises.

Figure 3

Two measures of stochastic amplification based on the PSD. The analytical PSD corresponding to the model parameters of figure 1 is shown. The first measure gives the system's overall sensitivity to noise and may be called overall amplification. It is calculated as the area under the PSD curve (the shaded area A₀), which is also the expected mean squared deviation of disease incidence from its mean value; that is, a measure of time-series variance. The second quantity is the coherence of the oscillations and measures the concentration of spectral power around the dominant endogenous frequency. A coherence value c can therefore be calculated as the spectral power associated with a defined range of frequencies around the peak (A_p) relative to the total area A₀, c=A_p/A₀. These two measures are plotted in figure 4a,c, respectively. Analytical expressions to calculate these quantities are provided in §2. These measures characterize demographically driven stochastic oscillations in the absence of seasonal forcing. The good qualitative agreement between the PSD calculated with and without forcing (figure 2; see also the electronic supplementary material) and the good correlation (not shown) with other general measures of amplification (Neubert & Caswell, 1997) suggest that this quantity also reflects the sensitivity to perturbations other than demographic noise, such as seasonality.

Figure 4

Amplification as a function of model parameters, both overall amplification and coherence. Various mappings of the parameter space are shown. (b) In the graph, the different dynamical regions are plotted (η=0). The boundaries between the regions change very little when a small but non-zero external immigration is considered (η=2×10⁻⁶ as in (a) and (c)), but notice that a hyperbolic-shaped instability boundary is introduced by such a process. (a) Overall amplification and (c) coherence (in percentage values) as defined in figure 3 are mapped into the parameter space. In (a), the curves correspond to the endogenous stochastic period calculated with the formula given in the electronic supplementary material. In (c), the instability boundary separating a sink phase, where the disease is maintained by external infections, from a source phase, where the disease is maintained by local transmission, is shown with a broken thick line. We have superimposed the different parameter values (Bauch & Earn, 2003b) for typical childhood diseases (triangles, measles; diamonds, whooping cough; circles, chicken pox; squares, rubella). Filled symbols represent values after vaccination. As has been suggested (Rohani et al. 1999; Keeling et al. 2001), whooping cough turns out to be the most unstable disease in this group; that is, the most sensitive to stochastic amplification. At the opposite extreme, measles shows better-structured, more coherent, cycles around the endogenous period and less overall sensitivity to stochastic amplification. In (b), we have also mapped other infections diseases (WHO, whopping cough; CHIK, chicken pox; RUB, rubella; MUM, mumps; MEA, measles; FLU, flu; SIPH, syphilis; data obtained from Olsen & Schaffer (1990), Dushoff et al. (2004) and Grassly et al. (2005)).