Bias in random forest variable importance measures: illustrations, sources and a solution
- PMID: 17254353
- PMCID: PMC1796903
- DOI: 10.1186/1471-2105-8-25
Bias in random forest variable importance measures: illustrations, sources and a solution
Abstract
Background: Variable importance measures for random forests have been receiving increased attention as a means of variable selection in many classification tasks in bioinformatics and related scientific fields, for instance to select a subset of genetic markers relevant for the prediction of a certain disease. We show that random forest variable importance measures are a sensible means for variable selection in many applications, but are not reliable in situations where potential predictor variables vary in their scale of measurement or their number of categories. This is particularly important in genomics and computational biology, where predictors often include variables of different types, for example when predictors include both sequence data and continuous variables such as folding energy, or when amino acid sequence data show different numbers of categories.
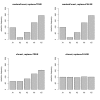
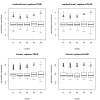
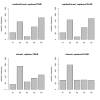
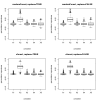
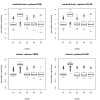
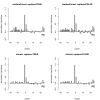
Results: Simulation studies are presented illustrating that, when random forest variable importance measures are used with data of varying types, the results are misleading because suboptimal predictor variables may be artificially preferred in variable selection. The two mechanisms underlying this deficiency are biased variable selection in the individual classification trees used to build the random forest on one hand, and effects induced by bootstrap sampling with replacement on the other hand.
Conclusion: We propose to employ an alternative implementation of random forests, that provides unbiased variable selection in the individual classification trees. When this method is applied using subsampling without replacement, the resulting variable importance measures can be used reliably for variable selection even in situations where the potential predictor variables vary in their scale of measurement or their number of categories. The usage of both random forest algorithms and their variable importance measures in the R system for statistical computing is illustrated and documented thoroughly in an application re-analyzing data from a study on RNA editing. Therefore the suggested method can be applied straightforwardly by scientists in bioinformatics research.
Figures
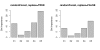

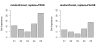

References
-
- Breiman L. Random Forests. Machine Learning. 2001;45:5–32. doi: 10.1023/A:1010933404324. - DOI
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Molecular Biology Databases

