A reaction-diffusion model to study RNA motion by quantitative fluorescence recovery after photobleaching

Abstract

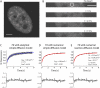
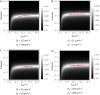
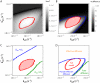
Fluorescence recovery after photobleaching (FRAP) is a powerful technique to study molecular dynamics inside living cells. During the past years, several laboratories have used FRAP to image the motion of RNA-protein and other macromolecular complexes in the nucleus and cytoplasm. In the case of mRNAs, there is growing evidence indicating that these molecules assemble into large ribonucleoprotein complexes that diffuse throughout the nucleus by Brownian motion. However, estimates of the corresponding diffusion rate yielded values that differ by up to one order of magnitude. In vivo labeling of RNA relies on indirect tagging with a fluorescent probe, and here we show how the binding affinity of the probe to the target RNA influences the effective diffusion estimates of the resulting complex. We extend current reaction-diffusion models for FRAP by allowing for diffusion of the bound complex. This more general model can be used to fit any fluorescence recovery curve involving two interacting mobile species in the cell (a fluorescent probe and its target substrate). The results show that interpreting FRAP data in light of the new model reconciles the discrepant mRNA diffusion-rate values previously reported.

FIGURE 1

Fitting FRAP curves with simple diffusion and reaction-diffusion models. (A) Cells expressing GFP-PABPN1 were imaged at 37°C. PABPN1 has a typical nucleoplasmic distribution with increased concentration in nuclear speckles. (B) For faster imaging during FRAP experiments, the number of lines is increased. Represented are images taken before bleaching, the first image after bleaching (t = 0 s), at t = 2.51 s, and at t = 7.57 s. Bleaching was performed in a circular region of 0.71-μm radius in the nucleoplasm (outside the speckles). The total nucleoplasmic radius at an equatorial image ranges between 5 and 12 μm. (C) The experimental data correspond to the average of three independent experiments with 10 cells analyzed per experiment (black lines). Error bars represent standard deviations of fluorescence values. According to the simple diffusion models (C and D), nonbound GFP-PABPN1 molecules and GFP-PABPN1 molecules bound to poly(A)-RNA are considered two independent populations; as most GFP-PABPN1 molecules are associated with RNA in the nucleus (see Discussion), the model assumed a single-component diffusion. In C, an analytical model was used (22), yielding estimates of the effective diffusion coefficient (D_eff) and immobile fraction (γ). In D, we used a numerical approach (see Results), which optimizes only for a single parameter, D_eff. According to the reaction-diffusion model (E), the bound and nonbound pools of GFP-PABPN1 molecules are in constant exchange. The diffusion coefficients of the free and bound species (D_F and D_C, respectively) are fixed parameters (see Results for justification of values) and the fitting procedure yields the off rate of the reaction (k_off) and the fraction of molecules bound to the mRNA (p). All fits (red lines) follow closely the experimental data and give similar minima for Σres². Below each fit are plots of the residuals showing that experimental values differ from the estimates by <10% in all cases.

FIGURE 2

Behavior of Σres² in the neighborhood of the minimum. The density graphs plot the values of Σres²as a function of the off rate of the reaction (k_off) and the fraction of molecules bound to the mRNA. The red line depicts points for which Σres² is <1% higher than the value of the absolute minimum, and the blue line depicts points that are < 0.1% higher than the minimum. In all graphs, Σres² varies steeply with p, whereas for k_off several values give results close to the absolute minimum. Thus, these data indicate that the optimal values of k_off are probably not bounded. No other local minima were found. (A) Using the expected values for the diffusion coefficients (as discussed in Results), D_F = 25.3 μm² s⁻¹and D_C = 0.04 μm² s⁻¹. (B) Increasing the mobility of the complexes 2.5 times, D_C = 0.1 μm² s⁻¹. (C) Decreasing the mobility of the complexes, D_C = 0.0 μm² s⁻¹. (D) Decreasing the mobility of the free molecules, D_F = 10.0 μm² s⁻¹. Though substantial variations were made in the diffusion components, fitting consistently found values around 20 s⁻¹ for k_off and >94% for p. In all the graphs, the minimum value of Σres² is the same (0.0137), i.e., it is independent of the values chosen for D_F and D_C.

FIGURE 3

Global view of the reaction space. k_off was varied between 2 × 10⁻³ s⁻¹ and 6 × 10⁺¹ s⁻¹ and between 2 × 10⁻³ s⁻¹ and 2 × 10⁺⁵ s⁻¹, and for each pair of k_off and a simulated FRAP curve was generated. All graphs are log-log plots for and k_off. (A) The density graph plots Σres² values for each reaction space point. The region delimited by the red line contains points for which Σres² > 0.03 (a threshold selected to qualitatively discriminate fits that were unsuccessful), indicating that inside this region a diffusion model is not able to properly fit data. (B) The density graph plots the difference between the predicted D_eff from Eq. 15 and the fitted D_est. The blue line contains the region for which a large disagreement (>20%) exists between estimates. Differences drop rapidly to small values outside this region. (C) The corresponding estimated diffusion coefficients. The green line shows the boundary of the region for which and the blue line the boundary of the region where (within a 5% tolerance). (D) Based on the findings from A–C, several regions can be identified: on the bottom right corner, the pure diffusion region; the full model region, where fits with a simpler diffusion model fail; the effective diffusion region,, in the upper part of the graph, where the diffusion model yields good fits, and simultaneously Eq. 16 is valid, and, finally, the pseudoeffective region, where good fits with a diffusion model are possible but Eq. 16 is not valid.

FIGURE 4

Influence of the reaction parameters on the effective diffusion coefficient measured. (A) An analytical diffusion model was used to fit simulated FRAP curves with varying p values. Log-linear plot of D_e versus p with constant k_off value used (22.2 s⁻¹). In this case, D_est is consistently much higher than D_C = 0.04 μm² s⁻¹, even if a large proportion (for example, 99.5%) of tagged molecules are bound to the substrate. (B) Superimposed over the domain structure of the reaction space (colored dashed lines), we represent: the points with the same D_est/D_C ratios (, , , , and 1.25) that are contained within the effective diffusion or pseudoeffective diffusion regimes. As expected for the effective diffusion regime, the lines obtained are straight lines along which the ratio is constant, located in the positions predicted by Eq. 15.