Dwell-time distribution analysis of polyprotein unfolding using force-clamp spectroscopy

Abstract

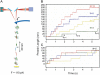
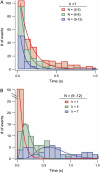
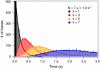
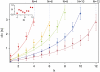
Using the recently developed single molecule force-clamp technique we quantitatively measure the kinetics of conformational changes of polyprotein molecules at a constant force. In response to an applied force of 110 pN, we measure the dwell times of 1647 unfolding events of individual ubiquitin modules within each protein chain. We then establish a rigorous method for analyzing force-clamp data using order statistics. This allows us to test the success of a history-independent, two-state model in describing the kinetics of the unfolding process. We find that the average unfolding trajectory is independent of the number of protein modules N in each trajectory, which varies between 3 and 12 (the engineered protein length), suggesting that the unfolding events in each chain are uncorrelated. We then derive a binomial distribution of dwell times to describe the stochastic dynamics of protein unfolding. This distribution successfully describes 81% of the data with a single rate constant of alpha = 0.6 s(-1) for all N. The remainder of the data that cannot be accounted for suggests alternative unfolding barriers in the energy landscape of the protein. This method investigates the statistical features of unfolding beyond the average measurement of a single rate constant, thus providing an attractive alternative for measuring kinetics by force-clamp spectroscopy.

FIGURE 1

Single molecule force-clamp experiments. (a) Schematic showing a polyprotein stretched under a constant force of 110 pN between the cantilever tip and the gold surface. The unfolding of a single domain is associated with a 20-nm release in the protein end-to-end length for ubiquitin. (b) Unfolding kinetics data for ubiquitin chains of varying number of protein modules, N. Length versus time traces show the 20-nm stepwise increase in length each time a single protein domain unfolds. Zero displacement is set at the point where the molecule is taught. The dwell times to the multiple unfolding events k are measured, as indicated in the trace with N = 3. Statistically, the larger the N, the shorter the time it takes to observe an unfolding event. (c) For a given N, the modules unfold within a range of times since the process is probabilistic. This gives rise to dwell-time distributions.

FIGURE 2

Comparison of the average unfolding trajectories obtained by summing over traces containing the same number of unfolding events N. The unfolding trajectories are independent of N, as obtained from the two-state fits of Eq. 1 to the data. The variation in the single exponential fits with a rate constant range 〈 α 〉 = 0.90–1.57 s⁻¹ arises from additional pathways in the landscape, also evidenced by the deviations of the single exponential fits with χ² = 40. The average trace over all the data is also shown with α = 1.03 s⁻¹.

FIGURE 3

Histograms of unfolding dwell times. (a) Distribution of dwell times to the first unfolding event, k = 1, as a function of N reveals that the waiting time is longer for chains with fewer ubiquitin modules. The curves are fitted with Eq. 3, which is the binomial distribution. (b) Distribution of dwell times for k number of unfolding events, for a fixed N range. The distributions range from exponential for k = 1 to normal for large k, characteristic of the binomial distribution.

FIGURE 4

Dwell-time distributions obtained using Monte Carlo simulations for 1000 traces with chain length N = 7. The success of the fits shows that a Markovian, two-state process with a single rate constant of unfolding gives rise to a binomial distribution derived in Eq. 3.

FIGURE 5

Fits of the experimental average dwell times as a function of k and N. Average dwell times to the first, second, k^th event in the sequence of each trace, segregated by the total number of steps in the staircase, N, show that the data is successfully fitted with Eq. 4, with a rate constant of α = 0.87 ± 0.13 s⁻¹. The error bars represent the mean ± SE. The variation in α shown in the inset is independent of N, confirming that the process is Markovian.

FIGURE 6

(a) Dwell-time distributions of experimental data that is best fitted with a single rate constant of α = 0.7 s⁻¹, consisting of 81% of all data. They are fitted with Eq. 3 as a function of both N and k, clearly indicating the success of the model. (b) Comparison of the average unfolding trajectories obtained by summing over: traces accepted by the iteration procedure (green line), and the outliers (red line). They reveal a clear separation in the rate constants (indicated in the legend) between the selected data and the outliers, suggesting a heterogeneity in the unfolding pathways. The single exponential fits still deviate from the two separated populations.

FIGURE 7

Thermal noise of the cantilever. (a) A typical unfolding length trajectory of ubiquitin, under a constant stretching force of 110 pN, shown in panel b. (c) The distribution of forces in the trajectory in panel b represents the thermal noise of the cantilever and gives an average force and a mean ± SD of σ_f = 6.82 pN. It broadens the distribution of measured rates of unfolding by 10% (see text) and cannot account for the outliers in the distribution.