The critical role of locomotion mechanics in decoding sensory systems

Abstract

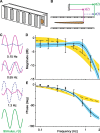
How do neural systems process sensory information to control locomotion? The weakly electric knifefish Eigenmannia, an ideal model for studying sensorimotor control, swims to stabilize the sensory image of a sinusoidally moving refuge. Tracking performance is best at stimulus frequencies less than approximately 1 Hz. Kinematic analysis, which is widely used in the study of neural control of movement, predicts commensurately low-pass sensory processing for control. The inclusion of Newtonian mechanics in the analysis of the behavior, however, categorically shifts the prediction: this analysis predicts that sensory processing is high pass. The counterintuitive prediction that a low-pass behavior is controlled by a high-pass neural filter nevertheless matches previously reported but poorly understood high-pass filtering seen in electrosensory afferents and downstream neurons. Furthermore, a model incorporating the high-pass controller matches animal behavior, whereas the model with the low-pass controller does not and is unstable. Because locomotor mechanics are similar in a wide array of animals, these data suggest that such high-pass sensory filters may be a general mechanism used for task-level locomotion control. Furthermore, these data highlight the critical role of mechanical analyses in addition to widely used kinematic analyses in the study of neural control systems.

Figure 1.

Identifying the whole-animal transfer function for longitudinal tracking behavior in Eigenmannia. A, The fish (brown) maintains its position within a rectangular tube. This refuge has a clear polycarbonate top and white plastic sides with ceramic-filled windows (gray). B, Schematic view of the video data captured using a camera positioned above the fish. Three values are the position of the fish [x(t), purple lines], the position of the refuge [r(t), green lines], and the relative difference between the fish and the refuge [e(t), dashed blue line]. C, Tracking data from a fish (stimulus amplitude, 0.5 cm). The height of each trace is scaled identically; the width of each trace is scaled to show two stimulus cycles (bottom; green) at three rates of motion (labeled). The amplitude of fish movements, x(t), decreased with increasing stimulus frequency with increasing phase lag. D, Bode amplitude. E, Bode phase plots for stimulus rates from 0.1–1.3 Hz. Error bars indicate the SD (N = 4 fish). The dashed curve indicates the first-order model (rejected), and the gold region indicates 95% confidence intervals for this model. The solid curve indicates the second-order model, and the blue region indicates 95% confidence intervals for this model.

Figure 2.

Closed-loop model of tracking behavior. A, Block diagram of the closed-loop control system including a model of locomotor dynamics and a neural multisensory controller, C(s). The locomotor dynamics can be modeled either using kinematics alone, 1/s (green), or using a model that includes mechanics, 1/Ms² (purple). B, Models of the C(s) filter; magnitude (in decibels) against frequency (in hertz). Kinematic locomotor plant predicts that C(s) is a low-pass filter (dotted green line); mechanical locomotor plant predicts that C(s) is a high-pass filter (dashed purple line). Tuning curves (blue lines; vector strength in decibels plotted against frequency) from ELL pyramidal neurons obtained under local (squares) and global (triangles) stimulus geometries (data from Chacron et al., 2003) match the high-pass filter prediction. All curves and data points are normalized to 0 dB.

Figure 3.

Stability and performance of the low-pass and high-pass controllers. Plots of the position of the fish over time are shown. The blue curve indicates the response of a fish to the novel increasing frequency stimulus: a frequency chirp. The dotted green curve indicates the unstable performance of the closed-loop model with a low-pass controller. The dashed purple curve demonstrates that the performance of the closed-loop model with a high-pass controller is similar to actual fish performance. Calibration: 1 s, 1 cm.