Robustness can evolve gradually in complex regulatory gene networks with varying topology

Abstract

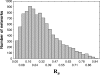
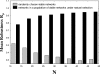
The topology of cellular circuits (the who-interacts-with-whom) is key to understand their robustness to both mutations and noise. The reason is that many biochemical parameters driving circuit behavior vary extensively and are thus not fine-tuned. Existing work in this area asks to what extent the function of any one given circuit is robust. But is high robustness truly remarkable, or would it be expected for many circuits of similar topology? And how can high robustness come about through gradual Darwinian evolution that changes circuit topology gradually, one interaction at a time? We here ask these questions for a model of transcriptional regulation networks, in which we explore millions of different network topologies. Robustness to mutations and noise are correlated in these networks. They show a skewed distribution, with a very small number of networks being vastly more robust than the rest. All networks that attain a given gene expression state can be organized into a graph whose nodes are networks that differ in their topology. Remarkably, this graph is connected and can be easily traversed by gradual changes of network topologies. Thus, robustness is an evolvable property. This connectedness and evolvability of robust networks may be a general organizational principle of biological networks. In addition, it exists also for RNA and protein structures, and may thus be a general organizational principle of all biological systems.

Figure 1. Regulatory Network Model and the Metagraph Concept

(A) A transcriptional regulation network. Solid black bars indicate genes that encode transcriptional regulators in a hypothetical five-gene network or gene circuit. Each gene's expression state is influenced by the transcriptional regulators in the network. This influence is usually exerted by binding of a transcriptional regulator to a gene's regulatory region (horizontal line). The model represents the regulatory interactions between transcription factor j and genes i through a matrix w = (w_ij). A regulator's effect can be activating (w_ij > 0, red rectangles) or repressing (w_ij < 0, blue rectangles). Any given gene's expression may be unaffected by most regulators in the network (w_ij = 0, open rectangles). The different hues of red and blue correspond to different magnitudes of w_ij. The highly regular correspondence of matrix entries to binding sites serves the purpose of illustration. We note that transcription factor binding sites often function regardless of their position in a regulatory region. (B) Gradual evolutionary changes and the metagraph. The middle panel shows a hypothetical network of five genes (top) and its matrix of regulatory interactions w (bottom), if genes are numbered clockwise from the uppermost gene. Red arrows indicate activating interactions and blue lines terminating in a circle indicate repressive interactions. The left-most network and the middle one differ in one repressive interaction from gene four to gene three (dashed gray line, black cross, large open rectangle). The right-most network and the middle one differ in one activating interaction from gene one to gene five (dashed line, black cross, large open rectangle). Each of the three network topologies corresponds to one node in a metagraph of network topologies, which is indicated by the large circle around the networks. These circles are connected because the respective networks are neighbors in the metagraph, i.e., they differ by one regulatory interaction. (C) Part of a metagraph for a regulatory network with N = 4 genes. Each node corresponds to a network of a given topology, and two nodes are connected by an edge if they differ at one regulatory interaction (M ≈ 0.5 N² regulatory interactions, and Hamming distance of S(0) and S _∞ of d = 0.5). The metagraph in this case is connected, and the number of edges incident on a node is highly variable. The graph shown includes all viable networks that differ at no more than four regulatory interactions from an arbitrary node in the metagraph. Note that metagraphs typically have a huge number of nodes. The number of nodes in a metagraph can be counted because different nodes differ only in the signs of their regulatory interactions.

Figure 2. A High Statistical Association between Robustness to Mutations and to Noise

The horizontal axis shows mutational robustness R_μ, which is the fraction of a viable network's neighbors (networks differing from it in only one regulatory interaction) that arrive at the same equilibrium state S _∞ given the initial state S(0). The vertical axes show two different measures of robustness to noise. The left vertical axis (+, solid line) shows R_{ν, 1}, the probability that a change in one gene's expression state in the initial expression pattern S(0) leaves the network's equilibrium expression pattern S _∞ unchanged. The right vertical axis (circles, dashed line) shows R_{ν, *}, the fraction of genes whose expression state in S(0) has to change at random, such that the probability that a network arrives at the equilibrium state S _∞ falls below a value of ½. In a network with large R_{ν, *}, perturbation of the expression states of a large fraction of genes affects the equilibrium pattern only rarely. R_μ is highly associated with both R_{ν, 1} (Spearman's s = 0.70) and R_{ν, *} (Spearman's s = 0.69, p < 10⁻¹⁵; 10³ networks for both). The sample is obtained from a Monte Carlo simulation as described in Methods (N = 20, M ≈ 0.25 N² regulatory interactions, d = 0.5, w_ij = ±1).

Figure 3. Heterogeneous Distribution of Mutational Robustness

The histogram shows the distribution of the fraction R_μ of neighbors of a network that differ at one regulatory interaction but attain the same equilibrium gene expression state S _∞. The data is obtained from a sample of 10⁴ networks (N = 20; M ≈ 0.5 N²; d = 0.7) sampled from the metagraph in a Monte Carlo simulation as outlined in Methods.

Figure 4. Natural Selection for Viability Dramatically Increases Robustness

The horizontal axis shows the number of genes per network. Black bars on the vertical axis show the mean mutational robustness R̄ _μ for populations under viability selection with PNμ ≫ 1, and grey bars show the mean mutational robustness R̄ _μ for a population with PNμ ≪ 1, in which selection for increased robustness is ineffective, and, thus, sampling of the metagraph is uniform (M ≈ 0.25 N², d = 0.5).