Assembly rules for protein networks derived from phylogenetic-statistical analysis of whole genomes

Abstract

Background: We report an analysis of a protein network of functionally linked proteins, identified from a phylogenetic statistical analysis of complete eukaryotic genomes. Phylogenetic methods identify pairs of proteins that co-evolve on a phylogenetic tree, and have been shown to have a high probability of correctly identifying known functional links.

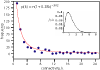
Results: The eukaryotic correlated evolution network we derive displays the familiar power law scaling of connectivity. We introduce the use of explicit phylogenetic methods to reconstruct the ancestral presence or absence of proteins at the interior nodes of a phylogeny of eukaryote species. We find that the connectivity distribution of proteins at the point they arise on the tree and join the network follows a power law, as does the connectivity distribution of proteins at the time they are lost from the network. Proteins resident in the network acquire connections over time, but we find no evidence that 'preferential attachment'--the phenomenon of newly acquired connections in the network being more likely to be made to proteins with large numbers of connections--influences the network structure. We derive a 'variable rate of attachment' model in which proteins vary in their propensity to form network interactions independently of how many connections they have or of the total number of connections in the network, and show how this model can produce apparent power-law scaling without preferential attachment.

Conclusion: A few simple rules can explain the topological structure and evolutionary changes to protein-interaction networks: most change is concentrated in satellite proteins of low connectivity and small phenotypic effect, and proteins differ in their propensity to form attachments. Given these rules of assembly, power law scaled networks naturally emerge from simple principles of selection, yielding protein interaction networks that retain a high-degree of robustness on short time scales and evolvability on longer evolutionary time scales.

Figure 1

Exponential and power-law curves. Illustration of exponential and power-law curves, showing how power-law generates a larger number of highly connected nodes. Two network diagrams illustrate hypothetical differences in network connectivity expected for random (exponential) and scale-free networks.

Figure 2

Phylogenetic tree of eukaryote species. Phylogenetic tree of fifteen eukaryote species used in this study (after Barker and Pagel, [10]). Dark blue dots illustrate hypothetical instances of a gene evolving and its protein entering the network; light blue dots illustrate instances of a gene and its protein being lost from the network.

Figure 3

Protein functional categories and protein network. Left panel. A comparison of the proportion of yeast genes (from MIPS database) in various functional categories and the 469 genes in the eukaryotic correlated evolution network. The two sets of proportions are highly correlated (r = 0.95), but proportions do differ (χ² = 33.8, p < 0.001). Right panel. The correlated evolution network describing 1774 A<=>B connections among the 469 genes, and its connectivity distribution well described by a power-law (r² = 0.98).

Figure 4

Connectivity distributions for gains and losses of proteins. Left panel: The connectivity distribution for genes at the time they enter the network. Based upon 174 genes that evolved after the root of the tree, and accounting for 395 new connections in the network (mean = 1.91 ± 1.77). Curve accounts for 95% of the variance in connectivity frequencies. Right panel: The connectivity distribution of genes at the time they were lost from the network. Curve accounts for 89% of the variance in frequencies. Based upon 239 genes comprising 847 losses or 3.54 ± 2.37 losses per protein (a protein can be lost in more than one place on the tree).

Figure 5

Acquisition of protein links and test of preferential attachment. Left panel. The relationship between the connectivity of a gene present at the root of the tree and its connectivity in the yeast (S. cerevisiae). Based upon 295 genes present at the root and in yeast. Line is 1:1 relationship. Right panel. The relationship between the number of connections acquired between the root of the tree and yeast (final-initial connectivity) and initial connectivity. Preferential attachment predicts a positive relationship. The regression line is positive but the weak relationship (r² = 0.03, slope = 0.018, p < 0.004), is not sufficient to produce a power-law scaled network (see text).

Figure 6

The variable rate of attachment model. Fit of the variable rate of attachment model (see text) fitted to the overall connectivity distribution of Figure 3 (right panel), accounting for 99% of the variance and illustrating that power-law scaling can emerge if proteins have different fixed propensities for forming attachments. Inset shows the predicted frequency distribution of attachment rates (α = 0.38, β = 3.02) under the variable rate of attachment model: most genes cluster around a low rate of attachment but a few show high rates of attachment, producing the 'hub' nodes in the network.