Evaluation of cortical current density imaging methods using intracranial electrocorticograms and functional MRI

Abstract

Objective: EEG source imaging provides important information regarding the underlying neural activity from noninvasive electrophysiological measurements. The aim of the present study was to evaluate source reconstruction techniques by means of the intracranial electrocorticograms (ECoGs) and functional MRI.

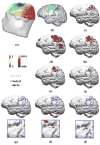
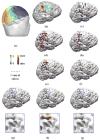
Methods: Five source imaging algorithms, including the minimum norm least square (MNLS), LORETA with L(p)-norm (p equal to 1, 1.5 and 2), sLORETA, the minimum L(p)-norm (p equal to 1 and 1.5; when p=2, the MNLS method is mathematically equivalent to the minimum L(p)-norm) and L(1)-norm (the linear programming) methods, were evaluated in a group of 10 human subjects, in a paradigm with somatosensory stimulation. Cortical current density (CCD) distributions were estimated from the scalp somatosensory evoked potentials (SEPs), at approximately 30 ms following electrical stimulation of median nerve at the wrist. Realistic geometry boundary element head models were constructed from the MRIs of each subject and used in the CCD analysis. Functional MRI results obtained from a motor task and sensory stimulation in all subjects were used to identify the central sulcus, motor and sensory areas. In three patients undergoing neurosurgical evaluation, ECoGs were recorded in response to the somatosensory stimulation, and were used to help determine the central sulcus and the sensory cortex.

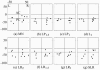
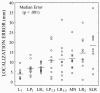
Results: The CCD distributions estimated by the L(p)-norm and LORETA-L(p) methods were smoother when the p values were high. The LORETA based on the L(1)-norm performed better than the LORETA-L(2) method for imaging well localized sources such as the P30 component of the SEP. The mean and standard deviation of the distance between the location of maximum CCD value and the central sulcus, estimated by the minimum L(p)-norm (with p equal to 1), L(1)-norm (the Linear programming) and LORETA-L(p) (with p equal to 1) methods, were 4, 7, 7 mm and 3, 4, 2 mm, respectively (after converting into Talairach coordinates). The mean and standard deviation of the aforementioned distance, estimated by the MNLS, LORETA with L(p)-norm (p equal to 1.5 and 2.0), sLORETA and the minimum L(p)-norm (p equal to 1.5) methods, were over 11 mm and 6 mm, respectively.

Conclusions: The present experimental study suggests that L(1)-norm-based algorithms provide better performance than L(2) and L(1.5)-norm-based algorithms, in the context of CCD imaging of well localized sources induced by somatosensory electrical stimulation of median nerve at the wrist.

Fig. 1

The procedure of the evolution of five CCD methods using the real EEG, ECoG recordings and fMRI results. The MNLS, LORETA-L_p, sLORETA, L_p-norm and L₁-norm (linear programming) methods are used in this study. In the LORETA and L_p-norm methods, the p value was set to 1, 1.5 and 2. Since the L_p-norm method of the Curry^™ 5.0 is based on the MNLS method, the MNLS-L_p (p=2) method is equivalent to the MNLS method in the mathematics. In this study, L₁, LP₁, LP_1.5, LR₁, LR_1.5, LR₂, SLR and MN expressed the L₁-norm (linear programming), L_p-norm (p=1), L_p-norm (p=1.5), LORETA-L_p (p=1), LORETA-L_p (p=1.5), LORETA-L_p (p=2), sLORETA and MNLS methods respectively.

Fig. 2

The evaluation procedure and method; d is the distance between the maximum point of CCD and central sulcus of cortex (Top view). (a) The maximum point of CCD and the central sulcus of cortex, (b) the maximum point of CCD and the central sulcus of cortex after converted into the Talairach coordinates. In the present study, d is calculated in the Talairach coordinates.

Fig. 3

Functional MRI activation obtained from one normal subject. (a) The motor task and (b) sensory stimulation. The right side of the green point is a knob-like structure, which is shaped like an epsilon in the axial plane. The central sulcus of the normal subject can be identified with functional MRI (a, b) and the gyrus structure.

Fig. 4

Results obtained using five CCD methods for patient #1. (a) The scalp potential mapping and the cortex; (b) the direct subdural ECoG recordings and the central sulcus; (c) SLR; (d) LR₂; (e) LR_1.5; (f) LR₁; (g) L₁; (h) MN; (i) LP_1.5; (j) LP₁. All CCD results are shown with a threshold set at 70% of the maximum current density (μA/mm²) or F-distribution value for SLR. The sLORETA is a statistical value (F-distribution) and others are CCD (μA/mm²).

Fig. 5

Results obtained using five CCD methods for patient 2#. (a) the scalp potential mapping and the cortex; (b) the direct subdural ECoG recordings and the central sulcus; (c) SLR; (d) LR₂; (e) LR_1.5; (f) LR₁; (g) L₁; (h) MN; (i) LP_1.5; (j) LP₁. All CCD results are shown with a threshold set at 70% of the maximum. The SLR is a statistical value (F-distribution) and others are CCD (μA/mm²).

Fig. 6

Results obtained using five CCD methods for normal subject 1#. (a) the scalp potential mapping and the cortex; (b) the maximum CCD point of all methods; (c) SLR; (d) LR₂; (e) LR_1.5; (f) LR₁; (g) L₁; (h) MN; (i) LP_1.5; (j) LP₁. All CCD results are shown with a threshold set at 70% of the maximum. The SLR is a statistical value (F distribution) and others are CCD (μA/mm²).

Fig. 7

Maximum CCD points in the Talairach coordinates, using the eight techniques from three patients and seven normal subjects. (a) MN; (b) LP_1.5; (c) LP₁; (d) L₁; (e) LR₂; (f) LR_1.5; (g) LR₁; (h) SLR. The physical units are mm. AC and PC are anterior commissure and posterior commissure, respectively

Fig. 8

Scatterplot of the localization error for the eight techniques tested. Horizontal line indicates median localization error for each technique.